Holly Freedman and Dr. Stephen Humphries, Microbiology
My project was to determine which elements of the symmetric group, or permutations on a finite set of objects, generate group representations for the braid group. I started out by finding group representations for the three-strand braid group. A three-strand braid is a set of three disjoint strings in three-dimensional space, whose height functions increase monotonically and which end at points vertically above where they start. The set of braids can be made into a group by letting one braid “multiply,” or perform an operation on, another braid by being placed above it, with their two sets of ends joined. The braid group on three strings is generated by two very simple braids x and y, which satisfy the relation xyx = yxy. In fact, this is the only relation needed in this braid group in the sense that all other relations follow from it. A group permutation representation of the braid group in the symmetric group Sn is a subgroup of Sn generated by two permutations x and y likewise satisfying xyx = yxy.
I tried two approaches at simplifying this problem. The first was to add the additional assumption that the two generators are cycles. I obtained examples of generators of representations of the threestrand braid group by computer. For each example, an associated diagram of vertices connected by line segments could be drawn; the vertices represented the objects being permuted and the line segments, the operation of the permutation. One cycle permutation was shown as a polygon, with its vertices further connected in a cyclic manner by line segments representing the other permutation. I analyzed these diagrams, looking for similarities. One pattern in particular seemed to show up in many of the diagrams. I was able to show why this pattern, seen in smaller diagrams, also occurs in diagrams with additional vertices. From this observation, I had the idea that two diagrams could be combined into a larger diagram, associated with another representation of the braid group. In this way, I was able to prove constructively that there are transitive non-abelian representations of the three-strand braid group in Sn for all n > 2.
Can any larger diagram be split into the “sum” of two smaller diagrams? This seemed to be possible for all of the examples which I had off of the computer, using one of three types of splitting. All of the examples of pairs of generators x and y obtained by computer also satisfied the relation (xyx)2 = 1. It would be interesting to know if this is necessarily always the case, but I was not able to prove it. However by assuming this additional relation, Dr. Humphries was able to show that all diagrams can be split in one of three ways. His reasoning was that xy and xyx are also generators of the same group that x and y generate. These generators have order three and two respectively; so their associated diagrams can be split rather simply, corresponding to splittings of the diagrams associated with x and y.
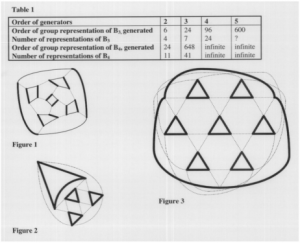
My second approach at simplifying this project was to classify conjugate sets of generators for representations of the braid group according to their order. At this point I widened my search to representations of the four-strand braid group. Generators x, y, and z of representations of this group must satisfy xyx = yxy, yzy = zyz, and xz = zx. I first required that the triplet of permutations x, y, and z generating a representation of B4 have order two, so that x2 = y2 = z2 = 1. Again, I considered diagrams associated with these sets of generators. We showed that only nine different connected patterns are allowed. One of these, which is in fact also a Cayley graph of S4 as generated by transpositions, is shown in Figure 1. I then moved on to sets of generators with order three. I found that there are five pairs of generators of transitive representations of the three-strand braid group, of order three. Two of these are shown in Figures 2 and 3. We used a computer to determine the orders of group representations generated by elements of order four and larger. We found that such groups have finite order if their generators have order four or five. This implies that there are only a finite number of possible connected diagrams, and places a limit on integers n such that there is a transitive representation of B3 in Sn generated by permutations of order less than six. See Table 1.