Nathan B. Holladay and Professor David D. Busath, Zoology
An ion channel is a tunnel that allows ions to cross a barrier. Ion channels are common components of cellular membranes, helping to regulate ionic concentrations in different areas inside or outside cells. Electrical and/or concentration differences between one side of a membrane and the other often drive the net flow of ions in one direction or the other across the membrane. Theoretical biophysicists have used computer-based molecular dynamics simulations for years now to study the behavior of ions within ion channels under equilibrium conditions. Before our study, however, few or no studies had been done in which molecular dynamics simulations were used to observe the movement of ions from solution into an ion channel and across the channel under the influence of a driving force.1 Claims by authors such as Eisenberg that such a study would be fraught with difficulty only increased my eagerness to complete one.
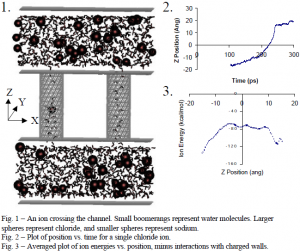
I used CHARMM26, a molecular dynamics program, to simulate the motion of ions in a system that included two parallel, fixed walls of atoms representing a membrane, along with two connecting pores and aqueous sodium chloride solution on either side of the “membrane” (see Fig. 1). Two charged, outer walls—one positive and the other one negative—provided a driving electrical force for the charged sodium and chloride ions. During calculations, “images”, or partial copies, of the central system (which is shown in Fig. 1) were present on the sides of the system in x and y directions (a slab geometry), so that the system would behave as if it were continuous in space. Different starting positions were used for ions in each of ten different runs. Each run was allowed to progress until at least one ion had passed through a channel, or until ions could no longer cross. Running time for each system on an SGI Origin 2000 supercomputer (donated to BYU by Ira Fulton) could exceed two weeks.
With data from two sodium and two chloride ion crossings, we observed that the trajectories of the ions traveling through the channels could be roughly divided into three segments. Upon entry, the ions proceeded slowly at first (see Fig. 2). This slow movement correlated to an increase in energy that the ions would have been experienced as they moved away from the bulk solution outside the channel, had the driving electrical force not also been present (see Fig. 3) As the ions moved closer to the center of the channel, their velocities increased, corresponding with leveling off of the energy of an ion passing through a channel without a driving force. Then as the ions approached the exit, this energy would start to drop, and they experienced further acceleration. The ion crossing time was about twice as long for the larger, negatively charged chloride ions, compared with the smaller, positively charged sodium ions.
During my research, I found that troubleshooting problems in original work is not always simple. For example, simulating an ion channel system such as ours requires calculation of electrostatic interactions between relatively distant atoms within the system. Without special treatment of these calculations, the simulations would run much longer. We discovered that the extended electrostatics method I used created an unnatural migration of certain ions toward the edges of the system. For such systems as ours with slab geometries, other methods, such as twodimensional Ewald sums3 would probably work better. This work has value, however, in giving some insight into the behavior of ions associated with channels and in being one of the first (perhaps the first) non-equilibrium molecular dynamics studies of an ion channel system with surrounding solution. It also demonstrates the possibility of using a slab geometry for such simulations, while showing how not to treat the electrostatic calculations.
References
- Eisenberg, R.S. 1999. From structure to function in open ionic channels. J. Membrane Biol. 171:1–24.
- Stote, R.H., States, D.H., Karplus, M. 1991. On the Treatment of Electrostatic Interactions in Biomolecular Simulation. J. de Chimie Physique. 88:2419–33.
- Yeh, I.-C., and M.L. Berkowitz. 1999. Ewald summation for systems with slab geometry. J. Chem. Phys. 111:3155–62.