Aaron Hart, Chia-Chi Teng and Drs. Richard Hopper, David Khechoyan, and Jennifer Brown

Abstract— Frontal-orbital advancement is the accepted surgical treatment for correcting the cranial deformity associated with premature fusion of one of the coronal cranial sutures. Removal and reshaping of the brow and lower forehead bone is performed to correct ipsilateral frontal flattening and parietal bulging, recession of the supraorbital rim, and contralateral forehead bossing. In addition to the functional aspects of the treatment, bilateral symmetry is one desirable outcome that is difficult to achieve because of the recessive movement and shape changes of the supraorbital rim that continue to occur over a prolonged period of time after the operation. Surgeons often over correct the deformity to compensate for post-operative recession and achieve better symmetry at skeletal maturity. This study is to quantitatively evaluate the stability and symmetry of the repaired supraorbital rim after the craniofacial reshaping procedures in patients with unilateral fusion of the coronal suture. CT scans taken at pre-op, post-op and two years later were available for digital analysis. Quantitative methods are developed to calculate the magnitude of advancement, magnitude of movement in the two years period following the surgery, and supraorbital bilateral symmetry at all three time points. Quantitative statistics of the post-op supraorbital rim stability will provide clinically relevant information for surgical planning that could optimize surgical technique.

Keywords-medical imaging; surgical planning; surgical outcome evaluation

I. INTRODUCTION

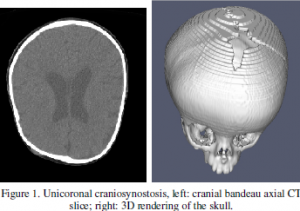
Unilateral craniosynostosis is the premature fusion of a coronal cranial suture, which resulting in deformity of the forehead and the face [1]. Frontal-orbital advancement is the accepted surgical strategy to correct the intracranial compression and provide space for the growth of the brain [2,3]. The aesthetic appearance is also normalized by restoring the bilateral symmetry at the supraorbital region (“bandeau”) and proper upper facial proportion. Figure 1 shows example cranial CT images of a patient with unilateral coronal craniosynostosis.

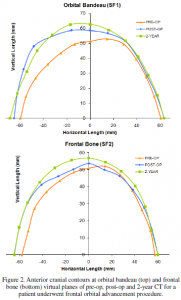
It has been observed that the post-operative shape and advancement of the supraorbital rim will change over time, resulting in progressive asymmetry, with an increased risk if the patients were operated at a younger age. Surgeons often attempt to compensate for post-operative retrusion by overcorrecting the magnitude of advancement on the affected side [4]. Figure 2 shows a patient’s 2D frontal skull contours on the axial cross section at the orbital bandeau and frontal bone locations from CT scans taken at pre-operation (pre-op), postoperation (post-op) and two years later (2-year); the subject’s bandeau shows better symmetry at 2-year compare to the postop CT.

The benefits of early surgical treatment for craniosynostosis patients have been documented in many studies [5]; however, the post-op stability of the supraorbital rim relating to age at operation is not well understood. The purpose of this study is to develop a method to quantitatively measure the magnitude of the advancement, symmetry and post-op retrusion over a two year period. By comparing the advancement and symmetry at pre-op, post-op and 2-year, we can assess the surgical outcome quantitatively. Having better understanding of the post-op stability of the supraorbital osseous bar may help us suggest optimal age at operation and surgical plans that would yield better long term results.

II. BACKGROUND

Little research has been done in quantitative outcome assessment for craniosynostosis surgery concerning cranial shape and appearance. Anderson and David [6] conducted a qualitative study on the late results after unicoronal craniosynostosis correction. The results suggested satisfactory long term functional result despite some persistent asymmetry.

Pai, Kohout and Mulliken [7] proposed a quantitative method to measure skeletal advancement and symmetry following frontal-orbital advancement. The measurement was not imaging-based, rather done by a surgeon with Castroviejo caliper during the surgery. It also does not include long term post-op data.

Lo, Marsh, Yoon and Vannier [8] conducted a quantitative analysis on stability of frontal-orbital advancement in bilateral coronal craniosynostosis using CT images taken at pre-op, post-op and one year later. While primitive measurements such as length:width ratio of anterior cranial fossa were used to assess ventral cranial morphology, more sophisticated shape and symmetry measurements were lacking.

3D CT scans are performed at pre-op, post-op, and 2-year according to the standard CT acquisition protocol at the Craniofacial Center in Seattle Children’s Hospital. Quantitative assessment of the cranial defect healing has been an ongoing research subject [9]. A study of cranial stability is a natural extension of the active research scope.

III. METHOD

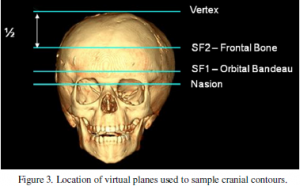
CT scans were first segmented to extract the 3D cranial surface models. Two virtual planes was chosen to represent the exterior shape of the forehead based on the anatomical landmarks: SF2 plane (frontal bone) was measured half way between cranial vertex and nasion, and SF1 plane (orbital bandeau) was measured one third the distance between SF2 and nasion as shown in figure 3.

Given a surface mesh M as the cranial surface model extracted from a set of CT scan, the cross sections between M and virtual planes SF1 and SF2 produced two 2D cranial contours CSF1 and CSF2. The most posterior and center point of the sella turcica is annotated as S with coordinate [xS, yS, zS] and the nasion as N with coordinate [xN, yN, zN]. The straight line connecting sella and nasion is designated as the SN line. The vertical projection of sella turcica on virtual 2D axial planes will just be S’ or [xS, yS].

Given {pi} as a set of sufficiently dense sample points on a 2D cranial contour C where i Î [1, n]. For each pi, its 2D Cartesian coordinate on the plane is (xi, yi), which can be converted to a polar coordinate (ri, qi) using S’ as the pole (origin), and projection of SN line as the zero polar axis as follows,

where qi Î (-p, p]. Only the anterior portion of contour C is of interests to us as we study the cranial stability after frontal orbital advancement or qi Î [-p/2, p/2]. The magnitude of the advancement and curvature at each polar angle can be aggregated to describe the shape and symmetry of the anterior cranial contours.

A. Advancement and Curvature

The magnitude of advancement at a polar angle can be calculated from the pre-op and post-op radiuses ri’s on the same polar axis. As all the polar coordinates from different CT scans are based on the sella and SN line, the difference between the ri’s is the magnitude of the advancement d, as the following, where dqpo is the magnitude of advancement at post-op time.

The advancement at 2 year later dq2y can be measured similarly.

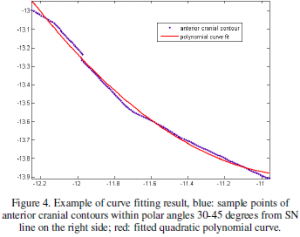
The curvature at a polar angle can be approximated through curve fitting. Given a subsection of cranial contour C or a continuous subset of {pi} where a <= i <= b, we can fit a quadratic polynomial function to the corresponding [xi, yi]. We use MATLAB Curve Fit Toolbox [10] to generate the polynomial function. If the difference of the two bounding polar axes of the subsection is less than 15 degree (or p/12 in radian), the error of the fit tends to be low and tolerable. For a quadratic polynomial function

its curvature is defined as

Figure 4 shows an example of the polynomial curve fitted to a subsection of a 2D cranial contour. Using the functions above, we can calculate the curvature at each pi on the subsection of cranial contour as

B. Stability

Stability of the repaired supraorbital rim can be derived from the change in radius or magnitude of advancement between post-op and 2-year anterior cranial contour at the SF1 and SF2 virtual planes. The change of advancement d two years after the procedure at polar angle q can be defined as,

where dq is the advancement measurement defined in Eq. (2).

We define the stability D of a subsection of the cranial contour between polar angles A and B as the following,

where rms is the root mean square of all the dq. A smaller D value corresponds to a more stable skull. 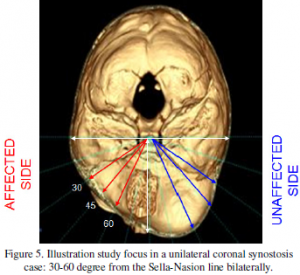C. Symmetry Index

Asymmetry between the two sides of the forehead has been associated with unicoronal craniosynostosis. Physicians use frontal-orbital advancement to reshape the skull and make it more symmetrical. A quantitative method is proposed to measure the bilateral symmetry of the front bone which can be used to evaluate the surgery outcome as well as the stability over the two year post-op period.

Symmetry index has been used to measure left-right symmetry in biomechanics research [11]. Given a subsection of the fontal cranial contour C defined by two bounding polar axes of non-negative angles A and B, it includes the subset of the {pi} on the right side where A <= qi <= B. The mirroring subsection on the left side consists of {pi} where -B <= qi <= – A. We can define the symmetry basis at polar angle qi as where XR, XL can be either the radius ri or curvature ki of the two corresponding points pi’s with the opposite qi on the right and left side as defined in Eq. (1) and (4).

The aggregated Symmetry Index SI between positive polar angles A and B can be defined as the root mean square of the symmetry basis of all pi within A and B as the following, where X could be the radius or curvature. SIR measures the symmetry in radius of the given subsection of the anterior cranial contour and SIC in curvature. A smaller SI value represents better symmetry and a zero SI is perfect symmetry,

IV. RESULTS

This study focuses on the critical region between 30 to 60 degrees from the SN line bilaterally as shown in figure 5. The stability and symmetry index are measured in fifteen degree intervals between 30 to 45 degree and 45 to 60 degree on the affected and unaffected side. 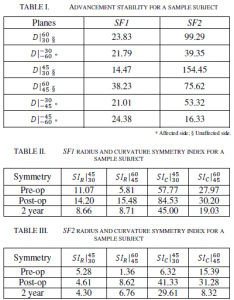Tables I-III show the stability and symmetry measurement for the sample subject shown in Figure 2. The positive polar angles correspond to the unaffected side and the negative to the affected side. Table I compares the stability of SF1 (bandeau) and SF2 (frontal bone) on the affected and unaffected side. As the stability D is inverse proportional to the advancement d as in Eq. 6, the D on the unaffected side may appear to be larger than the affect side simply because of the smaller d. While we have not studied enough cases to suggest a statistical pattern, quantitative measurement shows that SF1 is more stable than SF2 in this case. Various symmetry indexes at SF1 and SF2 planes of the same subject are listed in Table II and III respectively; two of which are shown graphically in Figure 6. We observed overall better symmetry in the 2-year CT then the post-op. However, smaller SI values are seen in certain pre-op measurement, e.g. SIr/60/45 in Table III because of the similar radius measurement as shown in Figure 6 (right) even though the contour shape is dissimilar. In which case the symmetry in contour (SLc) will display the higher value for the asymmetry in shape.

V. CONCLUSION

A quantitative study of supraorbital osseous bar stability and symmetry following frontal orbital advancement can help identify controllable factors (such as timing of surgery or surgical technique) that are associated with excessive surgical relapse. The proposed tools described above can now be used 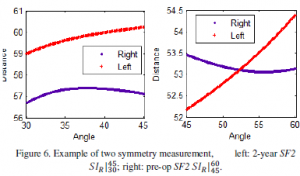to retrospectively analyze data from past unilateral coronal craniosynostosis cases performed at pediatric hospitals with standardized CT scan protocols. Quantitative results from these studies will help test hypotheses that have until now been based on anecdotal or subjective evidence. Examples include the appropriate age of patient at the time of operation, the benefit of using bone grafts to try to stabilize the advancement, and the relative value of unilateral verses bilateral surgical techniques. This approach will help direct an objective outcome-based approach to developing surgical care protocols for the treatment of unilateral coronal hypostasis.

REFERENCES

1. J. Panchal, V. Uttchin, “Management of craniosynostosis”, Plastic & Reconstructive Surgery, 111(6):2032-48, 2003.
2. L.A. Whitaker, S.P. Bartlett, L.Schut, D. Bruce, “Craniosynostosis: an analysis of the timing, treatment, and complications in 164 consecutive patiens”, Plastic & Reconstructive Surgery, 80:195-206, 1987.
3. G.E. Ghali, D.P. Sinn, S. Tantipasawasin, “Management of nonsyndromic craniosynostosis”, Atlas of the Oral and Maxillofacial Surgery Clinics, 10(1):1-41, 2002.
4. D. Marchac and D. Renier, “Craniofacial surgery for craniosynostosis”, Little Brown & Co, 1982.
5. D. Renier, E. Lajeunie, E Arnaud, D Marchac, “Management of craniosynostoses”, Child’s Nervous System, 16:645-58, 2000.
6. P.J. Anderson, D.J. David, “Late results after unicoronal craniosynostosis correction”, The Journal of Craniofacial Surgery, 16(1):37-44, 2005.
7. L. Pai, M. Kohout, J.B. Mulliken, “Prospective anthropometric analysis of sagittal orbital-globe relationship following frontal-orbital advancement in childhood”, Plastic & Reconstructive Surgery, 103(5):1341-6, 1999.
8. L.J. Lo, J.L. Marsh, J. Yoon, M.W. Vannier, “Stability of fronto-orbital advancement in nonsyndromic bilateral coronal synostosis: a quantitative three-dimensional computed tomographic study”, Plastic & Reconstructive Surgery, 98(3):393-405, 1996.
9. C. Teng, L.G. Shapiro, R.A. Hopper, J. VerHalen, “Pediatric cranial defect surface analysis for craniosynostosis postoperation CT images”, Proceedings of International Symposium on Biomedical Imaging, 620- 623, 2008.
10. http://www.mathworks.com/products/curvefitting/, last accessed on 10/27/2009.
11. D.J. Gales, J.H. Challis, “Evaluation of the assessment of symmetry during gait”, American Society of Biomechanics 2007 Annual Conference, 2007.
12. K.T. Paige, S.J. Vega, C.P. Kelly, S.P. Bartlett, E. Zakai, A.F. Jawad, N. Stouffer, L.A. Whitaker, “Age-dependent closure of bony defects after frontal orbital advancement”, Plastic & Reconstructive Surgery, 118(4):977-84, 2006.