Todd McCauley, Institute of Business Management
Introduction
The key to success In retail is a good store location. Several models have been developed to help retailers determine optimal store locations. This project is a store location simulation for a QuatroPro spreadsheet. The model is based on the Huffs Gravity Model, a well-known retail model, which states-in part-that a store’s revenues are based on its proximity to population centers.
My model performs some basic calculations that I have not yet seen in any of the models I have run across while studying this idea. Given a “map” of a city and the location of a competing store, this model calculates the revenues of a store located anywhere in the city. It is designed to calculate a store’s “revenues” for any location in the given grid. Each cell is assigned a number that represents the population of that particular block.
The Simulation
Michael Pearson and Glenn Stoops of Bowling Green University developed a model that stated that 30 percent of a store’s revenue comes from a 1-mile radius of the store, 30 percent from between one and two miles, and 10 percent from a three mile radius. I used a simplified model and used two radii; the cells are multiplied by a factor of .1 and .3 as shown below.
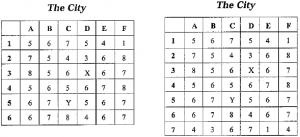
The following grid represents a city. Each quadrant is a city block with a specified population in the block. My store is represented by the”C”:, and my competitor’s store is marked by the “Y”. Each store has a “gravitational pull” on the surrounding blocks.
The adjacent blocks (the dark block) are affected by factor of .3 and the squares directly adjoining that block (the lighter block) are affected by a factor of, I, as shown below. The obvious strategy is, therefore, to place the store in a location that utilizes the largest population and avoid being too close to the other store. The value of this model is its ability to measure the total revenues that can be expected from placing the store in any quadrant given the population and the location of the other store.
Constructing the Model
In the spreadsheet, each cell is listed with the cells It affects. For example, cell d3 Is listed as follows:
D3=(c2,d2,e2,c3,d3,e3,c4,d4,e4,)* .3+(bl,cl,dl,el,fl,f2,f3,f4,fS,e5,d5,c5,b5,b4,b3,b2)* .1
The competition’s store Is listed as follows:
C5=(b4,c4,d4,b5,c5,d5,b6,c6,d6)*.3+(a3,b3,c3,d3,e3,e4,e5,e6,e7,d7,c7,b7,a7,a6,a5,a4)*.1
By using the function @sum the “value” of each store’s position can be calculated. However, the problem cannot stop here because of the “shared” cells. For example, cells c4 and d4 are in each store’s primary circle. Many of the other cells are shared by both stores as well. The trick in this project Is to determine a way to split the shared cells’ values.
The Results
The spreadsheet can determine the proper “score” for each store quite easily if one is willing to manually compare the cell components of each store, divide the shared cells’ values and add the new scores. I wanted to figure out a way to perform the process automatically so once the stores’ locations were determined, the answer would spit out automatically.
A cell location is reserved for the user of this program to type in his or her store location selection. Once that is typed in, the user must highlight the block that contains the that quadrant’s cell values (as shown above) with the mouse. The values refer back to the grid itself and add the numbers in the city cell blocks. This allows the user to change the population makeup of the city at any time without having to reprogram the simulation.
Once the block is highlighted, the user activates a macro and the value of the user’s particular location selection is displayed. the macro copies the block from the table listing all the cell values and repositions it below so the manipulations can be performed on that block to refigure its value considering the competitor’s claim on some of its cells’ values. By pulling it out of the main block before manipulating the score, the program can be run over and over. Each time the simulation is rerun the is restored to its original condition.
Once the blocks are pulled from the table, the spreadsheet determines the new store values. This is accomplished by running a search and replace command. I searched through each of my store’s cells for each of the competition’s cells and replaced them by a factor of 112. The list of the competitor’s cells are stored in memory and are called up in succession. For example, the first of the competitor’s cells is b4. I searched for cell b4 and replaced it with b4/2. The computer went to b4 found a 6 and divided it by 2. A 3 was therefore added to my equation for cell b4. The computer did that for each cell that was shared by both stores. I was able to go through the process manually and record each step as I went on a macro. By playing the macro back, the computer automatically mimicked my manual keyboard commands and determined the new scores. However, I did run into some snags I have not yet been able to resolve.
QuatroPro also has a problem running the search and replace command in the macro form. When it comes to a cell that is not shared, it quits searching and a new search must be run. the user~ therefore, has to run the macro for each cell search rather than performing it all in one fell swoop. I would like to program the macro to run the searches and jump over the unmatched cells.
The other improvement I am still trying to make is making this a two player game. I have not yet programmed a macro to figure the competition’s new score after the shared cells’ values are redetermined because, thus far, those cells have had to remain constant to measure against.
I plan on continuing to work on this project. I would like to program the ability into the program to handle several users at once and possibly more factors like store size into the program. I hope this project will be used in the retail class next year.