John Sutton Welch, Chemistry-Molecular Biology

During the last year I have examined numerical solutions and analytical approximations of the time-dependent Schrodinger equation for quantum systems with two, three and four levels which are perturbed by a classical sinusoidal field, I have been particularly interested in understanding the meaning and effects of the quantum phase on probability changes within the quantum system and have recently submitted my findings to the Journal of Chemical Physics and plan to present a poster of this and current work at the American Chemical Society meeting next April in Anaheim, California.

As I discussed in my proposal, the time-dependent Schrodinger equation has solutions of the form Cnexp(i8nt) where n labels the state; Cn are the time dependent amplitudes with real and imaginary coefficients of the n’h state and 8n is the time dependent phase (measured in degrees or radians) of the n’hstate. Until now, the amplitude C”‘ whose square gives the probability of the quantum system being in the n’h state, has enjoyed the main focus of research attention.

In my studies, I have found that phase coherency is an important element involved in causing the absorption and emission of energy from quantum systems. My research has revealed a surprising similarity between energy flow within a classical perturbing field and a quantum system and energy flow between two classical oscillators. Much like an adult pushing a child in a swing, the two parts of the system must be properly in phase for energy to flow between them. When the adult pushed the child just as the child reaches the top of her swing, she will swing higher and higher because the adult’s motion and the child’s motion are in phase. Likewise, when the sum of 81> 8n, (the phases of the lowest and highest states) and Ot (the frequency of the exciting laser times time) is zero, the system is “in phase” and energy is absorbed up into the highest state. However, when this sum changes by 1t radians, the system becomes out of phase, and energy is emitted out of the upper states down into the lower states. I have examined this for two, three and four levels systems, and it appears to be true in general.

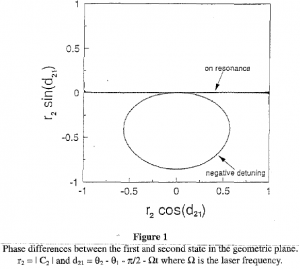
In an effort to better understand phase coherency, I developed a new geometric construct which represents the quantum phases in polar time-space. This construct is useful because it clearly distinguishes between zero and non-zero detuning and elucidates a fundamental difference between them. Figure 1 is a representation of the phase difference d21 (82 – 81 – n/2 – Ot) for a two level system where Q is the frequency of the sinusoidal laser and tis time. When the perturbing laser is tuned directly on the resonance frequency of the quantum system, the phase difference d21 moves back and forth along the x-axis because they-axis vector component is zero. However, when there is a negative detuning (Q < Qn), d21 has a both x- andy-directional components which causes it to precesses clockwise into the IV and III quadrants. With positive detuning (not shown) Q > 0 0 and d21 again has a y-directional component, but now it is positive and causes d21 to precesses counter-clockwise through the I and II quadrants. In either case, when there is detuning, a y-directional component causes the phase to drift away from the x-axis. As this happens, the phases drift apart and the 1st and 2nd states slowly become “out of phase.” With the states out of phase, probability can no longer be absorb from one to another. Thus, with a large detuning, the y-directional component of d21 will be strong enough to cause the phases 82 and 81 to drift apart quickly, and maximum probability of the system in the 2nd state will be minimal simply because the states are not in phase long enough to cause a complete population inversion. Although quantum absorption of energy has often been thought of as an instantaneous process, this suggests that it may be a relatively slow process that depends on subtle phase relationships being finely tuned.

This new construct has been extremely useful in elucidating a similar phase interaction in a multi photon system. Since 1931, processes have been studies which involve the absorption of two or more photons of similar frequency. The common perception of multi photon processes is that several discrete photons are absorbed more or less simultaneously. As I have expanded this geometric construct to examine multiphoton systems, it appears that it too is a gradual process; taking place over a relatively long time and one which requires that throughout the period many subtle phase relationships be maintained between each of the quantum states and the laser. If the physics described by the phase difference picture is correct, the phase stability of radiation fields which induce multiphoton transitions must be maintained for very long times to induce population inversion. It is then important to note that a phase change in the field will upset the phase relationship required to continue the process.

I am now evaluating the phase relationships involved in the use of pulse trains to achieve multilevel excitation. My findings thus far indicate that fine-tuned phase relationships are also critical for effective excitation in this system.