Donald M Cannon and Dr. Ross L Spencer, Physics and Astronomy
A plasma is a gaseous collection of charged particles. Although the particles move relatively independently, their interactions with each other as well as with externally applied fields result in collective behavior such as waves and turbulence. The complexity of this behavior has been one of the biggest obstacles in the development of nuclear fusion as an alternative power source as scientists have tried to understand and control the plasmas formed in fusion experiments. One of the characteristics of plasma behavior is the existence of normal modes. Just as different harmonics on a vibrating string can combine to form complex wave patterns, plasma states can be described as combinations of normal modes, with each mode possessing a specific frequency of vibration. In order to gain a more fundamental understanding of these modes and plasma behavior in general, it is helpful to look at the simple case of a cold, non-neutral plasma rather than more complicated hot plasmas containing ions, electrons, and neutral particles.
For a cold, non-neutral plasma in the presence of a uniform magnetic field, fluid models can be used to relate the electrostatic potential, f, of a plasma mode with the corresponding mode frequency, ù. Since exact analytic solutions to the mode equation don’t exist in most situations, Ross Spencer and I developed computer code to calculate approximate numerical solutions. By representing the coordinate space for the problem as a finite grid of points, solutions to the mode equation can be described by a vector containing the values of the solution at each point on the grid. The mode equation can then be approximated by the generalized eigenvalue problem Aφ=w2 /wp2Bφφ. Here A and B are matrices, φ is the solution vector, and wp is the plasma frequency (not to be mistaken with the mode frequency) as determined by the particle species in the plasma as well as the particle density in the plasma interior. Essentially, each row of the matrices is a finite-difference representation of the equation that is to be applied to a corresponding point on the computational grid. Since many commercial software packages can easily solve generalized eigenvalue problems, the difficulty in calculating the solution vectors lies in building the matrices A and B.
How you construct the A and B matrices depends on the coordinate system in which you formulate the mode equation. In developing our computer code, Ross Spencer and I considered plasmas that are confined within cylindrical traps. The geometry of these traps and the resulting equilibrium plasma shapes suggest cylindrical coordinates as the most natural coordinate system to use. In this coordinate system, the analytic form of the mode equation can be expressed rather simply. Unfortunately, traditional finite-differencing schemes for building the A and B matrices using a cylindrical coordinate system can’t be applied in a straightforward manner to the complicated plasma shapes that exist in the experimental situations we were considering. The most important reason for why this can’t be done is the need for the plasma boundary to lie on several grid points so that the condition dictated by the mode equation for the plasma boundary can be represented by one of the rows in the matrices A and B. The fact that uniform rectangular 57 grids are used results in a small likelihood that the plasma boundary is going to lie close enough to an adequate number of grid points. Ross Spencer and I determined that one way to get around this problem is to create a new (albeit non-orthogonal) coordinate system in which one of the coordinate surfaces corresponds to the plasma boundary. In other words, if we go from the cylindrical coordinate system with points (r,z) to one in which the points are defined by, say, (ñ,s), then we can choose the definition of ñ and s such that the constant surface ñ=1, which is a straight line in our new coordinate system, corresponds to the plasma boundary. This simpler geometry allows us to construct a rectangular computational grid such that one of the rows of points corresponds exactly to the plasma boundary.
Unfortunately, the definitions of ñ and s make it so that the boundaries associated with the walls of the trap no longer follow straight lines in the new coordinate system. However, we found that the condition φ=0 that is to be applied along the wall boundaries can be approximated by using a unique least-squares approach. To do this, we first used a bilinear interpolation function to approximate the function φ in the cells containing segments of the trap wall. We then integrated the value of φ2 across the wall boundary and then chose values of φat grid points outside the physical solution space such that this integral was minimized.
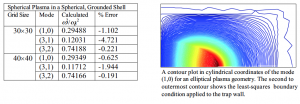
To determine the accuracy of our numerical representation of the mode equation in the (ñ,s) coordinate system, Ross Spencer and I compared our results for the simple case of a spherical plasma within a grounded spherical shell to corresponding analytic solutions. Results and percentage errors for different mode frequencies are listed below. To test the least-squares boundary condition along the actual cylindrical trap wall, we made several contour plots of our solutions in the cylindrical coordinate system and found that the interpolated value of φwas indeed near zero along the wall of the trap.
Although Ross Spencer and I have been pleased with the results we have obtained up to this point, several items still need to be addressed in our research. The first is the need to incorporate equilibrium plasma shapes into the calculations and improve our computer code’s ability to efficiently handle higher-resolution grids. Once this is done, we will address the need to minimize the effects that occur in higher resolution grids when modes with similar frequencies begin to become numerically indistinguishable from each other and overlap. Eventually, we hope to produce an easy-to-understand package of software tools that plasma researchers can use to make mode calculations. These calculations can then become the basis for additional work in the field of plasma physics.