Mark Lyon and Dr. Brent L. Adams, Mechanical Engineering
Using methods described by Adams1, the design of a compliant beam was modeled in a multidimensional Fourier design space. A compliant beam is one that achieves motion through bending. The motivation for the problem was a bicycle derailleur. A compliant beam could replace the entire rear derailleur if a large amount of flexibility could be obtained and yet have a relatively strong force when displaced to return the beam to its original position. The compliant derailleur would be simpler and cheaper than current derailleur designs. In general, metals are too stiff and plastics are too weak for this application. The performance of metal components can be improved or degraded by the material’s microstructure.
The analysis done in this paper used a nickel beam although the technique can be applied to any crystalline material. In order to improve the flexibility of a compliant beam, the microstructure may be taken into consideration. The individual nickel atoms are arranged into repeating cubic structures. A grain is grouping of these structures in which the orientation of the cube is constant. Most metals are made up of millions of randomly orientated grains. The distribution of the orientations of the grains can have a large effect on material properties. For our purposes we define the microstructure to be orientation distribution of the grains in the metal.
The range of all possible orientation distributions was modeled in a Fourier space using surface spherical harmonic functions with cubic symmetry defined by Bunge2. The sum of all the possible orientations forms a material hull in this design space. The design constraints were also modeled in this design space as hyper planes passing through the hull. The intersection of the design constraints and the material hull represents one or more microstructures that meet all of the design requirements. Collection of the hyper plane intersections on the outer limits of the material hull would then yield the range of performance available for the compliant beam.
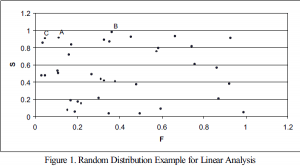
Collection of these limits requires linear analysis to determine optimal microstructures. Due to the nature of the problem it can be shown that an optimal solution consists of only one or two distinct orientations. By discretizing the set of all possible single orientations and calculating the both the Fourier terms for flexibility and strength relative to the beam axis for each orientation, a data set is produced that can be analyzed to get a representation of the performance closure for the compliant beam. By setting a value for flexibility of the beam, any orientation with that flexibility or any pair of orientations where one has orientation has greater flexibility and the other has less is a solution to for that flexibility. To find the maximum strength at a given flexibility one could consider a two dimensional plot of the data (see Figure 1). One axis would be the Fourier coefficients for flexibility (F) and the other the Fourier coefficients of strength (S).
Using Figure 1, if the F we wish to obtain is 0.35 then the first step would be to obtain the highest S with F equal to 0.35. Point A is quickly identified. Next a line can be formed from A to any point with F greater than 0.35. The angle of this line can be efficiently calculated. The maximum angle is obtained between A and B. Once point B has been identified, the algorithm can search all F less than 0.35 again in order to improve the height of the line. Point C is identified as a slight improvement over A. Since a new point on the left has been chosen the right must be analyzed again but no combination exceeds B-C. The relative proportions of B and C can then be calculated using the distances B and C are from 0.35. This analysis must be done in terms of Fourier coefficients because they can be added linearly.
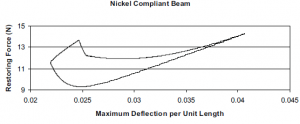
Once completed for a given value of F, F is incremented until the full range of F has been explored. In a similar manner to that described above, the solution for minimum values of S can be obtained by simply inverting the data before the algorithms loop. Figure 2 shows the analysis with Nickel for the entire performance closure of the compliant beam.
References
- Adams, B. L., Henrie, A., Henrie, B., Lyon, M., Kalidindi, S.R., Garmestani, H., 2001,“Microstructure-Sensitive Design of a Compliant Beam”, J. Mech. Phys. Solids, In Press.
- Bunge, H. J., 1993, Texture Analysis in Materials Science, Cuvillier Verlag, Goettingen.