Ryan J. Larsen and Dr. Brent L. Adams, Mechanical Engineering
Much research in recent years has focused on producing polycrystalline materials with high numbers of special grain boundaries. Special grain boundaries are defined as boundaries with desirable properties, such as resistance to corrosion, cracking, or precipitation. Most researchers describe grain boundary geometry only with the three parameters of misorientation between adjacent crystal lattices. Although misorientation data have been successfully linked to some properties, knowledge of misorientation alone is insufficient to predict grain boundary energy, and can thus provide only a first-order approximation of a boundary’s properties.
What is clearly missing from most current studies of grain boundaries is knowledge of the orientation of the grain boundary plane. A grain boundary plane orientation together with a crystal misorientation provides the five parameters necessary to completely constrain the macroscopic geometry of the boundary.
Recovering grain boundary plane orientations is difficult because in a typical two-dimensional data set, the boundary plane appears as a single trace. Traditional methods of grain boundary orientation recovery, such as serial sectioning and TEM studies, are presently too time consuming to produce data sets that are large enough to be statistically reliable. Hilliard1 and Adams2 have proposed stereological methods for recovering boundary distributions in the sample reference frame. Both methods require observations of grain boundary traces on a number of oblique section planes cut from the sample.
Despite the usefulness of these stereology techniques, no method has been proposed to recover grain boundary plane orientation distributions in the crystallographic frame of an adjacent grain. Knowledge of the grain boundary plane in the crystal frame of an adjacent grain is useful because it contains information about the arrangement of atoms near the boundary, thus helping the researcher characterize boundary energy and other properties.
By discovering and implementing an original application of the stereological relationship developed by Adams2, we have developed a powerful new technique for recovering the distributions of grain boundary planes in the crystal frame. This can be accomplished with data retrieved from a single section plane of material! A description of the new method is beyond the scope of this paper and will be the subject of a future publication.
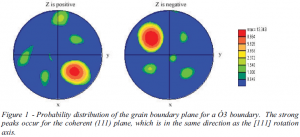
The figure below shows the probability distribution of grain boundary plane normals obtained from sixty-four grain boundary traces taken from a single section plane of AISI Type 304 Stainless Steel. All sixty-four boundaries belong to a special and common family of boundaries known as Ó3s. A Ó3 boundary is simply a 60 rotation about a rotation axis in a direction. A boundary’s classification as a Ó3 boundary is independent of the orientation of the boundary plane.
Although the grain boundary plane in a Ó3 could, in principle, be oriented in any direction, it is known that there exists a preferred low-energy grain boundary orientation for Ó3 boundaries. This is known as the coherent or habit plane. Crystallographically, the coherent plane normal for a Ó3 boundary is in the same [111] direction as the rotation axis.
The sixty-four boundaries used to recover the function shown below were all strong candidates for being coherent Ó3 boundaries. This is because each trace was 1) long compared to the average grain size, 2) very straight (a characteristic of coherent Ó3 boundaries) and 3) nearly perpendicular to the coherent (111) plane normal. Thus, we are very encouraged to observe strong peaks (shown in red) in the recovered function at the (111) coherent positions. This result demonstrates that our new technique produces results that are very reasonable.
The secondary peaks shown in green and yellow are residuals of the surface spherical harmonics used to calculate the function shown. They exist because the function shown is only mapped to 6th order. Solving the higher-order coefficients of the function will reduce the size of the secondary peaks and make the primary coherent peaks become narrower and higher.
This new technique is exciting and groundbreaking. This is the first time that probability distributions of grain boundary normals in the crystal frame have been recovered from a single section plane. The technique promises to have a significant impact on the world of grain boundary engineering by providing the Material Scientist with previously unobtainable information about the probable orientations of grain boundary planes in the crystal frame.