Eric L. Peterson and Dr. Ross L. Spencer, Physics and Astronomy
Research groups at BYU and the University of California at San Diego (UCSD) are actively investigating the properties of pure-electron plasmas, which fall into the more general class of nonneutral plasmas. Electrons are excited and injected into a Malmberg-Penning trap where they form a cylindrical plasma. By perturbing the confining electrical potentials of the trap, various wave motions can be induced in the plasma. Some of these waves exhibit a phenomenon called Landau damping which transfers energy from the wave motion to the kinetic energy of the electrons, causing the wave to attenuate.
The theory of the wave damping mechanism of interest to this report was first discovered by L. D. Landau [1]. Landau damping occurs in two phases, linear and non-linear and is sometimes called collisionless damping because the wave is damped without energy dissipation due to collisions. The Landau mechanism depends entirely on the distribution of velocities among the plasma particles and in particular on particles close to “resonant” velocities. A particle has a velocity resonant with the wave if it interacts with the wave at the same place in its phase every time an interaction occurs. During the linear phase of Landau damping the wave amplitude decays exponentially until a saturation point where the non-linear phase begins. During the nonlinear phase the amplitude of the wave oscillates, with the particles and wave alternately giving and taking energy. Figure 1 below shows a trace of a wave damped by the Landau mechanism.
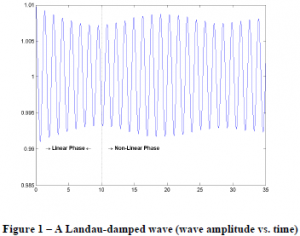
Experiments with Landau damping at BYU and UCSD resulted in wave frequencies that were predicted accurately by usual textbook theory [2,3]; however the wave damping rates were significantly lower than theory predictions. One effect that is not taken into account by the normal Landau theory (which assumes a plasma of infinite extent) is the finite-length of the plasma and the resulting interaction of plasma particles with the moving ends of the plasma. In my ORCA-supported investigations (which were part of the completion of an honors thesis) I studied two simplified situations to shed light on the effects of these considerations. The first situation is a hard plate (or “manhole cover”) suspended above kinetic gas particles. This situation is considerably easier to model because there are no electromagnetic fields involved. Figure 1 – A Landau-damped wave (wave amplitude vs. time) The second situation replaced the hard plate with one made of rubber, so that particles have a finite turnaround phase when they reach the top rather than instantly bouncing back. This more closely models the real pure-electron plasma, where the particles turn around in the ends of the plasma due to the electric potential pushing them back into the plasma region.
By varying the temperature and density of the particles that suspend the plate it was possible to observe Landau damping in both of the situations just described. I developed computer simulations in C++ to track the motions of the plate and the millions of gas particles supporting it and in collaboration with my mentor we produced theories for each scenario. We found that our theories and numerical simulations showed superb agreement, both in the predicted wave frequency and damping rate. Figures 2 and 3 show results obtained for the hard plate scenario. The results for the simulations and theory of the rubber plate scenario showed similarly excellent agreement.
Finally, there is one more step to complete in this project. The particles need to become charged and electrostatically confined. The plate needs to be removed to be replaced by the edge of the plasma, and both a simulation and a theory need to be developed. The presence of the selfconsistent electric field will make the analysis much more difficult but the simulation should be straightforward.
References
- L. D. Landau. J. Phys. (USSR), 10:25, 1946.
- F. Chen. Introduction to Plasma Physics and Controlled Fusion, volume one. Plenum Press, New York, NY, second edition, 1984.
- D. Nicholson. Introduction to Plasma Theory. John Wiley & Sons, Inc., New York, NY, 1983.
