Kenton R. Wride and Dr. Gilbert W. Fellingham, Statistics
The stated mission of the World Health Organization (WHO) is to improve health around the world. One aspect of this mission involves preparing reliable models to describe patterns of health world wide. WHO has built a summary data file based on nearly 700 published and unpublished reports of anemia rates of women worldwide. Fellingham et. al (1996) prepared a preliminary report of the first model developed from this data as well as the resulting estimates of world wide anemia. The study was based on 448 records from 83 countries. The data included the mean hemoglobin concentration, sample size, a country identifier, the region of the country in which the study was carried out (1-urban, 2-rural, 3-national sample) (area), the pregnancy status of the subject participants (1-pregnant, 2-not pregnant, 3-national sample) (pregnant), the number of calories ingested per capita in the country as a proportion of daily requirement (thus this number often exceeded 100 in industrialized nations) (calories), the percentage of illiterate females in the country (pcillitf), the percentage of females in the country receiving some sort of prenatal care (prenat), the percentage of deliveries occurring in a health care facility (instdel), the percentage of deliveries attended by some sort of health care provider (attdel), the status of malaria transmission in the country (0-none, 1-moderate, 2-severe) (malaria), the amount of money in U.S. dollars expended on health care per capita (dolpcap), and the altitude of the study site (0-sea level, increasing by increments of 0.5 for altitude increases of 500 meters) (altit).
WHO requested that additional and more accurate data be incorporated into the original model constructed by Fellingham et. al (1996) to produce revised estimates of world wide anemia. Anemia rates are measured by the hemoglobin concentration in the blood (hg). As part of this project, a fertility variable provided by WHO was added to the covariates, and the altitude data was updated with new data also provided by WHO. Because the analysis would require us to know the number of subjects living in urban an rural environments, and the number of pregnant and non-pregnant females in a given country, this data was also obtained. The percentage of pregnant females was computed based upon females of child bearing age and birth rates in a country. The next step involved the building of matrices and models such that the coefficients for the models’ variables could be easily interpreted. The actual model building was done using SAS Proc Mixed using the weights option with weights equal to sample size. We have not been able to test the assumption that hemoglobin concentration follows the normal distribution because a suitable dataset has not yet been provided by WHO for this purpose. The original model included area, preg, area by pregnancy interaction (axp), calories, pcillitf, instdel, attdel, malaria, dolpcap, and altit as fixed effects. Random effects included country (conum), country by area interaction (conum*area), country by pregnancy interaction (conum*preg), and country by area by pregnancy interaction (conum*axp).
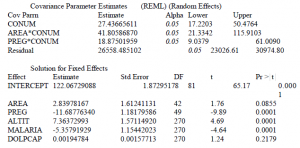
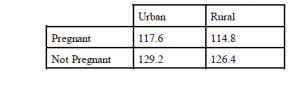
A somewhat reduced model which we believe best fits the data has variance components which were significantly different from 0, and fixed effects which induced a significant decrease in the log likelihood when they were removed from the model. This model includes area, preg, altit, malaria, conum, area*conum, and preg*conum. The other variables did not significantly affect hemoglobin concentration. Estimates of the fixed effects as well as covariance parameter estimates of random effects are shown in Table 1. This model indicates that concentration of hemoglobin in the blood should increase by roughly 7 grams/liter for every 1000 meters of elevation, should increase .00195 g/l for every $1 increase in per capita health expenditures in a country, and should drop 10.6 g/l in a country with severe malaria transmission. It seems that the correction for altitude is an underestimate since any missing altitude data was considered to be at sea level. The differences attributable to area and pregnancy are shown in Table 2.
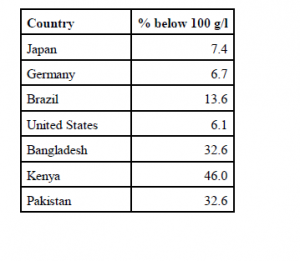
Estimates of the proportion of women who fall below the critical hemoglobin level of 100 g/l are found in Table 3. In summary, the model verifies that the area in which one lives, pregnancy status, altitude, status of malaria transmission, and the dollars spent on health care per capita are important variables in estimating hemoglobin concentrations (anemia rates) in women.
Table 1: Selected Proc Mixed output for the fitted model where HG concentration is the dependent variable
Table 2: Expected mean concentration of Hemoglobin in grams per liter, by area and pregnancy in
a country with no malaria, at sea level with zero dollars expended per capita on health care.
Table 3: Estimate of the percentage of women whose hemoglobin is below the critical level of 100
for selected countries.