Matthew Earp and Dr. Stephen E. Benzley, Civil and Environmental Engineering

Finite Element Analysis (FEA) is a method of performing mathematical analysis on complex geometry used extensively by both scientists and engineers. An important step in performing the analysis is the mesh generation process. This is the process of dividing a volume into small individual elements (finite elements). Currently there are two common shapes for these elements: tetrahedrons and hexahedrons. Due to the fact that tetrahedrons are a much simpler geometric shape, many robust tetrahedral meshing algorithms have been produced and find a wide range of uses. For solid modeling problems however, hexahedrons are the element of choice. Unfortunately there has been less success in developing robust meshing algorithms for hexahedrons. Because of this, much more effort is needed to produce a hexahedral mesh, often requiring hundreds of man-hours.

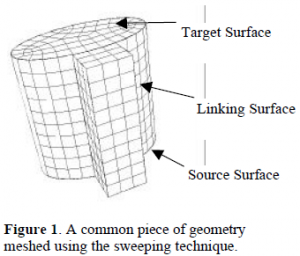
One proven method of hexahedral mesh generation is the sweeping technique.1 The sweeping technique works by dividing an object into a source surface, a target surface and multiple linking surfaces. The linking surfaces are meshed with a regular quadrilateral grid and the source surface is meshed using general surface meshing techniques. The mesh on the source surface is then propagated (swept) through the volume to the target surface creating an allhexahedral mesh in the volume. A volume meshed using the sweeping technique is shown in Figure 1.

Another helpful technique for mesh generation is grafting. The grafting algorithm is designed specifically to handle secondary volumes attached to the linking surfaces of previously meshed geometry. This algorithm works by distinguishing between the meshed (base) volume and unmeshed (graft) volume. The mesh on the joining surface of the base volume is then adjusted to conform to the source surface of the graft volume. Then the meshed source surface is swept through the graft volume. These steps are illustrated in Figure 2.

Although sweeping is the most robust hexahedral meshing technique, it is limited to extruded objects. However, in an effort to combine sweeping with grafting, a meshing tool was produced with the ability to sweep objects containing changing crosssections with the added potential of multi-axis sweeping. This tool is called the GraftSweep tool.

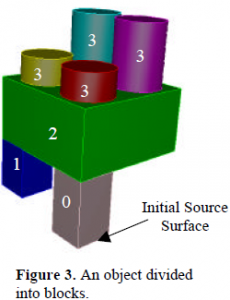
The GraftSweep tool works by taking an object that is not sweepable and dividing it into sweepable blocks. In this geometry decomposition process, the blocks are also numbered based on the distance of their source surface from the initial source surface. A geometric model that has been divided into blocks is shown in Figure 3.

Once the object has been divided into blocks, the meshing process can begin. This is done by selecting the block with the lowest number and sweeping it. Once this is accomplished, any blocks immediately above the swept block must be grafted onto the swept block. This establishes a continuous mesh between all the blocks. After the first block has been swept, the block with the next lowest number is selected for meshing, and the process starts over. Blocks with the same number can be meshed in any order. Meshing is completed when the last block has been swept. Three objects that were meshed using the GraftSweep Tool are shown in Figure 4.

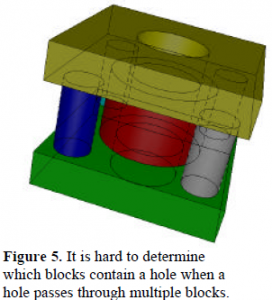
One difficulty that was discovered with the GraftSweep process is meshing objects with holes in them. Although it is not hard to find the beginning or end of a hole, the difficulty arises when a hole propagates through multiple blocks as shown in Figure 5. When this is the case it is hard to determine which blocks contain the hole. Currently, research is being done to solve this problem and a tool with the ability to handle holes should be available in the near future.2