Bradley C. Bundy and Dr. Larry Lin Baxter / Hugh Bradley Hales, Chemical Engineering
Oil is one of the most important commodities we have. It provides energy, transportation, and chemicals to provide a better life for mankind. However, it is a depleting recourse that is getting harder and harder to find and recover. Simulation techniques have been used for many years to determine the best place to drill wells and when it is the best time economically to stop pumping slurry. Unfortunately, current simulators often take weeks to months to complete and are only an estimate of what may occur. The industry is currently limited by slow, inaccurate simulation techniques. Faster simulators with increased accuracy have the potential to substantially increase profits for oil companies and decrease environmental damage by decreasing the amount of “dry wells” dug.
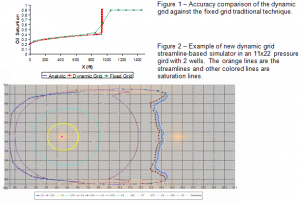
In this research, a fully functional new streamline-based novel dynamic grid reservoir simulator has been developed . The simulator is 100s of times faster than the typical simulator used currently in industry, which uses the traditional finite difference method, because the new simulator uses streamlines. The speed advantage of using streamlines in oil reservoir simulation is because streamlines make the currently used very complex three-dimensional equation that is solved using numerical computation techniques into a simpler one-dimensional equation. The new technique also has the advantage of greater accuracy by using a dynamic grid. Oil reservoir simulators use a grid of pressures to solve for the velocity, direction, and concentration of oil flow. The current method uses a fixed grid, or a pressure grid that does not account for changes in pressure as oil is pumped out of the reservoir. By using the dynamic grid, the pressure grid is updated continuously by using Cory’s Equations. Because the underlying pressure grid is more accurate with the dynamic grid, the proposed dynamic grid simulator has created simulations with greater accuracy.
To prove the accuracy of the new technique, three different solutions of the oil saturation were calculated along one streamline or in one-dimension given the same pressure and velocity conditions. The results are found in Figure 1. The analytical solution or Buckley-Leveret solution was considered to be the exact solution. As demonstrated by Figure 1, the dynamic grid solution (from the simulator developed in this paper) has a three times more accurate a fit to the analytical solution than the fixed gird solution (from the traditional finite difference solution).
Another advantage of the new streamline-based simulator is its ability to incorporate such effects as gravity, capillary pressure, relative permeability, and compressibility, which previous streamline-based simulators, such as the analytical solution, have not been able to successfully incorporate. The new streamline-based simulator also has the advantage of unconditional stability over the traditional fixed grid finite difference solution. Unconditional stability allows the new simulator to take larger time steps, while the traditional fixed grid technique will become unstable, oscillate, and crash the computer if too large of a time step is used.
To create such a novel streamline-based oil reservoir simulator using a dynamic grid, the following steps were performed:
1) Geological data was incorporated in a data processing program.
2) This data along with equations describing the pressure changes in an oil reservoir, such as the Darcy equation, were incorporated to create a two-dimensional pressure grid.
3) By using other physical equations (with the potential to incorporate gravity, capillary pressure, compressibility, and all other non-linear effects) the positions and velocities of streamlines were calculated from the pressure grid.
4) The dynamic grid method was used to solve for the saturations and concentrations of oil along the streamlines.
5) The saturations were then used to calculate mobility values along the streamlines using a modified Cory Equation.
6) The new mobilities were used in the equations used to calculate the pressure grid and thus update the pressure grid. This step caused the simulator’s grid to be dynamic in nature.
7) The procedure is repeated with each new time step.
By deriving the equations necessary and creating a reservoir simulation program that followed the above steps, the speed and accuracy of streamline simulation did increase. As mentioned previously this new simulator has the potential to save oil companies millions of dollars and decrease the amount of oil wells required.