Rachelle Curtis and Dr. G. Bruce Schaalje, Statistics

Introduction:

In the Semiconductor industry, it is necessary to compare the performance of different test-tapes to assure that each produces similar quality work. Test tapes sort each die, or computer chip, into one of a fixed number of bins, depending on how well it functions. When validating a new test tape, several die are tested using both the old and the new test tape and the bin assignments are compared. Kappa, a statistical measure of agreement, compares the number of matching bin assignments to the number expected if the test tapes are independent. Unfortunately, the closer Kappa is to one (perfect agreement), the more unstable the estimator for the variance of Kappa becomes, causing traditional confidence intervals, based on the Normal Distribution, to be inadequate. The objective of my project was to find a confidence interval for Kappa that is still reliable when Kappa is close to one.

Literature Review:

Upon examination of the literature, I found that although the unreliability of traditional confidence intervals for Kappa is a recognized problem, not many alternative solutions have been suggested. In addition, all of the simulation studies that have been done are for the binomial outcome case. Because there are more than two bins that a particular die can be assigned to, the binomial outcome case is not appropriate for this application.

Flack (1987) compared four confidence interval techniques. From her simulation studies, she determined that the Edgeworth skewness correction method, based on the Jacknife variance estimate, and the square-root transformation method improved the actual confidence level obtained for one-sided confidence intervals when Kappa is non-zero.1

Lee and Tu (1994) expanded upon Flack’s ideas. They compared the square-root transformation method, used by Flack to two additional confidence interval techniques based on the profile variance. Based on their simulation studies, they concluded that the method based on the profile variance after reparameterization outperforms the other methods.2

Until recently, SAS, a statistical software program, could only compute confidence intervals for kappa and weighted kappa based on the standard variance estimate. At the March SAS Users Group International meetings, Vierkant (1997)3 presented a SAS macro for calculating confidence intervals about kappa or weighted kappa using bootstrap resampling methodology.

Methodology:

Based on the review of the literature, I decided to compare four different confidence interval methods for Kappa in the multiple outcome case. These included the standard method, based on the normal distribution, the square-root transformation, the jacknife and the bootstrap. Both the jacknife and the bootstrap methods use variances based on different resampling techniques. Within the bootstrap, two submethods were used.

A simulation program was written in SAS to compare the different sampling techniques. For each iteration of the program, a data table was generated based on a probability table with a known kappa. The estimated kappa and a 95% confidence interval using each of the methods was constructed. Because a “good” confidence interval is one that is small and includes the actual parameter value a large percentage of the time, the methods were compared based on coverage rates and average confidence interval lengths.

The probability table used in 1120 simulations trials was 6 by 6 and had an actual kappa value of .90. Because the number of die tested in a test-tape comparison is usually large, a sample size of 100 was used.

Results:

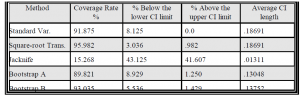
The results of the simulation study are summarized in the table below. The technique with the best coverage rate was the square-root transformation method, however the bootstrap B method was very close. The Jacknife had the smallest average confidence interval length, however its coverage rate was extremely poor. Of the two methods with approximately the same coverage rate, the bootstrap B method had the smallest average length.

Conclusions:

Based on this data, the bootstrap B method appears to be the best overall because it has a relatively high coverage rate and small confidence interval length. I plan to continue this project as my master’s thesis and will look at the effect of different sample sizes, varying kappa values, and more simulation trials. I also plan to look at operating characteristic charts for each of the methods examined.

References:

1. V. F. Flack. 1987. Communications in Statistics 16(4): 953-968.
2. J. J. Lee and Z. N. Tu. 1994. Journal of Computational and Graphical Statistics 3: 301-321.
3. R. A. Vierkant, SAS Users Group International Conference, 1997.

Table 1: Simulation Trial Results