Deborah L. Paulson and Dr. Ross L. Spencer, Physics and Astronomy
When a cloud of charged particles is contained in a Penning Trap, it can be observed to flatten into a disc. The measurement of physical properties of these pancake-like plasmas, such as density and temperature, is difficult or impossible without destroying the plasma in the process. In order to determine such physical properties, it is necessary to find a relation between an observable quantity and the other physical properties of the plasma. The observable quantity is the frequency of a normal mode of oscillation.
A theory proposed by Daniel Dubin 1 at the University of California at San Diego related ratios of the mode frequencies of a cold, uniform density, spheroidal plasma to the aspect ratio, or shape, of the plasma. When Dubin’s theory was tested by Weimer 1 et al in an experiment at the National Institute of Science and Technology in Boulder, Colorado, there was a 20% discrepancy between the measured and predicted results.
There have been several unsuccessful attempts to account for this large of a discrepancy. In the winter of 1995, I worked with Dr. Ross Spencer to determine the effect of a non-ideal containment field on the plasma shape. This, unfortunately, could only account for a fraction of the discrepancy. Other work was done by members of my department in studying the effects of image charges in the walls of the trap. This consideration actually led to a worse discrepancy. 2 It has been the intent of my research this year to study the actual density distribution of a warm plasma in global thermal equilibrium, in order to test whether the non-zero temperature of the plasmas in Weimer’s experiment was the cause of the discrepancy.
Computation of the plasma density profiles involves a two-dimensional solution of Poisson’s Equation in cylindrical coordinates. Fortunately, in the experimental limit that the plasmas are very thin, it is possible to separate the axial and the radial parts of the equation. The axial equation is not difficult to do numerically, which leaves only the radial equation to solve.
In order to solve the radial equation, I have written a FORTRAN code which uses an adaptive integrator and Powell’s method for minimization. I have also included constraints on the particle number and the canonical angular momentum, both of which must be conserved. The code uses a form for the profile which I have built into the program, varying the parameters within the form in order to find the profile which will give the lowest error in the electrostatic calculation.
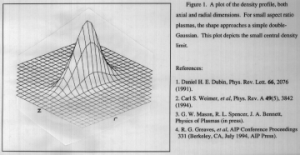
A careful study of the numerical data as well as the governing equations has revealed many interesting patterns which lead to a deeper understanding of the problem. In the experimental limit of extremely thin and relatively warm plasmas, the non-linear set of integral equations reduces to a set of simple linear equations which predict the values of several of the parameters, as well as giving an analytic solution to the problem for very small aspect ratios. After this limit was discovered, I tested the numerical code to see if it would yield the predicted results. As I decreased the aspect ratio for a fixed temperature, the profile did approach the predicted Gaussian limit.
(See figure.) This research, which has been the starting point for my masters thesis, is interesting for several reasons. Applications in the field of chemistry include studies of trapped ions in a magnetic field, where a knowledge of the density profile is important for studying chemical reactions. A similar application is in the study of matter-antimatter annihilation, such as when electrons and positrons are contained in a trap. Knowledge of the density profiles is also important for my research, because it will make it possible to determine the mode frequencies of the plasmas in order to compare to Weimer’s experiment.
The results of this research will soon be prepared for publication, at which point I will begin my analysis of the dynamics of the oscillating plasmas. I am optimistic about the potential of this research to not only explain the discrepancy between Dubin’s theory and Weimer’s experiment, but to provide a method by which the mode frequencies of oscillating plasmas can be used to determine their physical properties.
References
- Daniel H.E. Dubin, Phys. Rev. Lett. 66, 2076 (1991). 1
- Carl S. Weimer, et al, Phys. Rev. A 49(5), 3842 (1994). 2
- G.W. Mason, R. L. Spencer, J.A. Bennett, Physics of Plasmas (in press). 3
- R.G. Greaves, et al, AIP Conference Proceedings 331 (Berkeley, CA, July 1994, AIP Press).