Spencer Shore and Dr. Anton Bowden

Introduction

Burst fractures are high-speed spine injuries caused by rapid axial compression of the vertebrae. The traditional explanation for the burst fracture mechanism points to an intraosseous pressure rise due to the entrance of the intervertebral disc through a fractured endplate. Recent experiments [1], however, indicate an actual decrease in both internal pressure and hydraulic resistance in high-speed tests that result in burst fractures. These results cast doubt on the validity of the traditional burst fracture theory. The current study seeks to model the intraosseous pressure rise using the finite element method. In this model, the trabecular core and marrow of the vertebrae are modeled as a single biphasic material using an experimentally determined hydraulic permeability. It is hypothesized that this characterization will more accurately model the effects of intraosseous pressure rise in the formation of spinal burst fractures.

Methods

A quarter symmetry model of an idealized lumbar functional spinal unit was developed using averaged geometric data of lumbar and lower cervical cadaveric specimens reported in the literature. The model included cortical and cancellous bone, superior and inferior bony endplates, nucleus pulposus and annulus fibrosis sections. The bony segments were modeled as linear elastic materials with moduli and densities obtained from the literature. The nucleus was included using a hyperelastic Mooney-Rivlin type constitutive equation with constants C1 = 0.5 and C2 = 0.05.

In order to account for the directional fibers in the annulus fibrosis, a transversely isotropic Mooney-Rivlin material model was used [2]. The coefficients for this model were derived by the optimization of a finite element model to reported axial and circumferential stress-stretch data for the annulus fibrosus [3].

For the cancellous section, a biphasic material model was utilized to represent both the trabecular bone and marrow. This formulation requires only the permeability of the material to implement a second fluid phase on top of the existing solid phase [4]. The entire model was solved using FEBio (Musculoskeletal Research Laboratories, University of Utah), an implicit, nonlinear finite element solver specifically designed for applications in biomechanics.

The permeability used for the biphasic, cancellous portion of the vertebrae was drawn from the experimental results of Ochia and Ching [5]. In their paper, they reported a hydraulic permeability of 4.90×10-10±4.45×10-10 m2 for human lumbar vertebrae.

A two stage approach is used to model the burst fracture response. The present work reports on the first stage (low displacement rate results). For this study, the top face of the model was displaced downward at a constant rate of 5 mm/s for 0.2 seconds in order to match the low displacement rate results reported by Ochia and Ching [6].

Results

Initial results on simplified geometry show an altered pressure distribution (Figure 1) and overall higher intravertebral pressures (Figure 2) for the biphasic model as compared to the standard elasticity model.

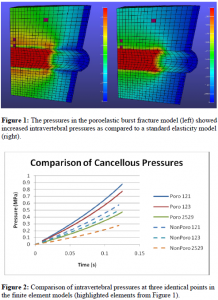
Discussion

These results indicate the potential advantage of a biphasic characterization and move toward the second phase of creating higher fidelity geometric models to be run at the high displacement rates typical of in vivo burst fracture events.

Acknowledgements

This work funded through a mentored environment grant provided by Brigham Young University.

References

• Ochia R, Ching R (2006), 31(22):2569-2574, Spine.
• Weiss JA, et al (1995), 135:107-128, Comp Meth Appl Mech Eng.
• Guerin HL (2007), 25(4):508-16, J Orthop Res.
• FEBio Theory Manual.
• Ochia R, Ching, RP (2002), 124:533-537,J Biomech Eng. [6] Ochia R, Ching, RP (2002), 27(11):1160-67, Spine.