Nathan Moon and Dr. Bryan S. Morse, Computer Science
A set of points in three dimensions can be tetrahedralized, or broken into non-intersecting tetrahedra, in many ways. A Delaunay tetrahedralization of a set of points is a tetrahedralization with the property that the sphere defined by each tetrahedron in the structure does not contain any other points in the structure besides the points defining the tetrahedron. A Delaunay tetrahedralization of a set of points is unique except for the case where more than four points are co-spherical.
Delaunay tetrahedralizations, and their dual, the Voronoi diagram, are important for many applications. Geometric modeling, like terrain modeling, is one example. In our case, we were using Delaunay tetrahedralizations in research of a new color quantization algorithm for digital images.1
Because of speed problems with the color quantization algorithm, we needed to be able to remove a point from a Delaunay tetrahedralization without being forced to re-compute the entire tetrahedralization. Delaunay tetrahedralization algorithms have a running time of, at best, O(n). Being forced to re-compute the entire tetrahedralization on each iteration of the algorithm made the running time O(n2).
We searched the literature for an existing algorithm to remove a point from a Delaunay tetrahedralization in O(1), or constant, running time, and were unable to find reference to anyone having implemented one. We did find algorithms for removing a point from a two-dimensional triangulation, and originally planned on extending the most commonly used algorithm, described by Martin Heller, to three dimensions.2
We discovered that Heller’s two-dimensional algorithm did not extend to three dimensions because it made assumptions that did not hold in the three dimensional case. We then set out to develop an algorithm that would work in three dimensions.
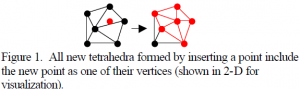
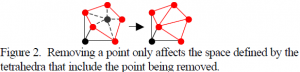
The algorithm we developed is based on one of the basic properties of a Delaunay tetrahedralization. This property has to do with the changes that occur to the structure when a new point is added. When a new point is added, all of the tetrahedra that are formed during the insertion have the new point as one of their vertices (figure 1). Thus, removing a point from a Delaunay tetrahedralization only affects space defined by the tetrahedra that have the point that is being removed as one of their vertices (figure 2). It is important to note that the space defined by these tetrahedra is not necessarily convex. The algorithm is as follows:
1. Remove all the tetrahedra that have the point to be removed as one of their vertices.
2. Tetrahedralize all the points included in these tetrahedra (except the point to be removed, of course) separate from the original structure. The resulting structure is convex.
3. Remove any tetrahedra in the new structure that correspond to concavities in the space defined by the original tetrahedra.
4. Merge the two structures together.
The tetrahedralization created by this method is guaranteed to be Delaunay. Because the property that this algorithm is based on does not depend on the number of dimensions, this algorithm should extend to n dimensional Delaunay triangulations.
Because the number of tetrahedra affected by this algorithm is, in practice, independent of the size of the structure, the running time of deleting a point with this algorithm is constant, or O(1). Using this algorithm reduced the overall running time of the color quantization algorithm from O(n2) to O(n), or linear running time.
Since the development of this algorithm, we have discovered a recently published paper outlining a different algorithm for removing points from a Delaunay tetrahedralization.3 This paper also pointed out the problems with Heller’s algorithm, showing that the algorithm fails in two-dimensions as well. The proposed algorithm is simple, and extends easily to n dimensions.
References
- B. Morse, T. Howard, S. Larson, M. Bastian, and E. Mortensen. Color Quantization and Dithering Gamuts. Proceedings of the IASTED International Conference on Signal and Image Processing (SIP’99).
- Martin Heller. Triangulation Algorithms for Adaptive Terrain Modeling. Proceedings of the 4th International Symposium on Spatial Data Handling, pages 163-174, July 1990.
- Olivier Devillers. On Deletion in Delaunay Triangulations. SCG, pages 181-188, Miami, Florida, 1999.
