Michael I. Kellogg and Dr. Russell Daines, Mechanical Engineering

Space is the final frontier. That has been generally believed since Sputnik went up in the 1950’s, but in spite of this optimistic belief, homesteaders have not yet begun to settle Mars, nor have businesses sponsored ventures to other planets. One of the reasons that the final frontier is so quiet is the prohibitive expense of getting there. Currently it cost about $10,000 to launch a pound of payload into low earth orbit.1 NASA, in an effort to lower the cost of launching payloads into space, has been encouraging researchers to develop alternative launch vehicles to replace the Space Shuttle. One promising new technology being investigated is the rocket based combined cycle (RBCC) engine. Through the use of RBCC engines, and other new vehicle related technologies, researchers hope to reduce launch costs by two orders of magnitude.1 The RBCC engine in its simplest form is a rocket placed inside of a duct. Figure 1 shows the schematic of a typical RBCC engine. It is potentially cheaper to operate than an equally powered rocket, because it combines the benefits of an air breathing engine with the benefits of a rocket engine to produce more thrust for less effort. By being cheaper to operate then a rocket, the RBCC engine promises to reduce the cost of launching payloads into orbit.

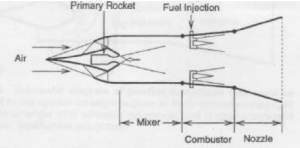
The RBCC engine is more efficient than a rocket because it can function as a rocket and as three different types of air breathing cycles. The type of air breathing cycle it operates in depends upon which is the most efficient for the current flight velocity. These different types of air breathing cycles are: ejector-rocket mode, ramjet mode, and scramjet mode.

Modeling the RBCC

Research is currently being done on the RBCC engine and computational fluid dynamic (CFD) models are being created to facilitate that research. At Pennsylvania State University CFD models have been created for the ejector-rocket mode of the RBCC engine1. Areojet built a test engine and has also focused on the ejector-rocket mode. A global model of the ejector-rocket has been created there to predict what configuration of rocket and duct produces the greatest thrust3. Research done at BYU for this ORCA project was focused on confirming the results of this global analysis.

One of the problems faced when attempting to confirm Areojet’s model is that it assumes that the pressure of the entrained air is the same as the exit pressure of the rocket when they mix. It also assumes that the ejector-rocket is ideally expanded, or in other words, the exit pressure of the whole ejector-rocket engine equals the atmospheric pressure. These are important assumptions because when pressures are equally matched like this, the maximum thrust is produced. The difficulty arises because the method of achieving this pressure matching is still under investigation by the people at Pennsylvania State who have not yet published their results. In order to confirm the conclusions of Areojet’s model using CFD models, it is important to be able to control the stream pressures inside the ejector rocket, and to predict the exit pressure. An attempt was made at BYU to determine a method of predicting the pressure of the air stream. From the results of this study, CFD models were created to verify the global analysis.

Method

Both analytical and CFD techniques were used to determine the effect of the duct area to rocket area ratio and the rocket expansion on the thrust of the ejector-rocket. First a global analysis was done, based on Mel Bulman=s analysis, using modern one-dimensional compressible flow theory, which predicted what configuration gave the greatest thrust. Then CFD models were created to verify that configuration. Once the grid density required for grid independent solutions was determined, CFD models were created that held the rocket expansion constant and varied the area ratio, and that held the area ratio constant but varied the rocket expansion. From that data a rocket expansion and area ratio was determined which produced the greatest thrust. Data from these models was also used to develop a theory for controlling the mixing pressures. This theory, while primitive, was used to develop CFD models, based on the global analysis, which varied both rocket expansion and area ratio simultaneously to determine which configuration gave the most thrust.

The global analysis was done in Excel, and the CFD code DUNS was used to solve the numerical models. Post processing tools were also used to analyze the results of the models. The grid was generated using 2DMBLK, a 2-D grid generator.

Results

Both the global and the numerical analysis showed us that, for a rocket expanded to induce a secondary Mach number of 0.85, the same thrust can be achieved in a smaller duct than could be achieved by any other rocket expansion in a larger duct. In the case of the modeled rocket, inducing a secondary Mach number of 0.85 occurs when it is optimally expanded to have a rocket exit Mach number of 3.7813, or an Ae/A* of 15.685.

Conclusions

One of the major conclusions that can come from this analysis is that for this particular rocket, it was predicted that an expansion to Mach 3.78 will produce the most thrust regardless of duct size. This result is for an ambient pressure of 98.59 kPa.

Another important result of this study is a greater understanding of what is needed to achieve pressure matching in an ejector-rocket. It was shown that entrance length and exit length don’t seriously affect it, but area ratios, rocket expansions, choking the flow, and allowing the shock train to dissipate all have an important effect on the pressure. Hopefully this work, together with that of researchers around the world, will help make it possible for us to reach for the stars.

References

1. Uwe Hueter, ACreating an Airline To The Stars,@ Areospace America, April 1999, pp. 40-44.
2. R. Daines, C. Segal, “Combined Rocket and Airbreating Propulsion Systems For Space-Launch Applications” Journal Of Propulsion and Power ,14.5, 1998. pp 605-612.
3. Correspondence through Dr. Russell Daines at Brigham Young University.