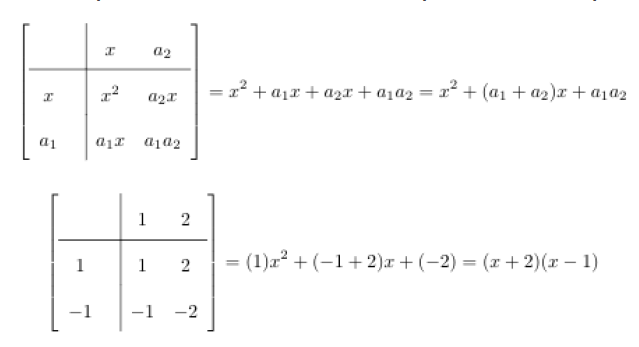Catherine Sawyer, Tyler Jarvis, Mathematics

Introduction

The purpose of this project was to develop a method by which sets of multivariate polynomials with known roots could be rapidly generated. Generating such polynomials would be of great use in testing root finding algorithms, yet remains an open problem

Methodology

Polynomial interpolation is a well-studied problem in the one-dimensional case. We therefore began by attempting to extrapolate existing onedimensional interpolation methods to higher dimensions. We investigated several methods, including the naive approach and a new method that we developed.

The naive approach to interpolation in one dimension, that of multiplying roots together in the form (x-a1)(x-a2)…(x-an), already fails in the twodimensional case. Even the simple problem (x-a1)(y-a2) yields roots along lines, rather than at a single point.

The method we developed took the following form:

For the problem (x+a1)(x+a2), set up a matrix such that one part of the equation is along one axis, and the other along the other. As shown in the image below, this type of matrix multiplication would allow for matrix computations in a computer, and by following the diagonals of the multiplication, could extend to higher degree polynomials. We tried to extend this method to higher dimensions, but were unable to find a way to do so.

Discussion of Results

Because all of the methods we explored were unsuccessful, we suspected that the problem might not be solvable. We consulted with Simon Tellen, an expert in the field. After much consideration, Tellen informed us that perfectly square systems – systems with the same number of roots as independent variables – occur with probability 0 as the dimension increases.

Ultimately, polynomial interpolation from known roots continues to be a widely recognized open problem. Our results were significant in that we clarified several ways in which this problem cannot be solved. Other parts of our group’s project, such as developing a viable root finder, are ongoing, and will continue to receive much effort and attention.

Discussion

Independently of its results, this project was a tremendous learning experience for me.

Involvement in this project provided me an understanding of how solutions to research problems are pursued. I learned how to read academic papers, and most importantly, I learned how to consider the idea that problems are not always solvable. This is a lesson that I could not have learned in my classes, since the problems in homework assignments are always solvable. I also learned that “failure” is not synonymous with “a waste of time”, and am grateful to be able to carry that lesson with me in my future endeavors.

Conclusion

Albert Camus once said, “the struggle itself towards the heights is enough to fill a man’s heart.” To me, this means that there is inherent worth in working towards an unsolvable problem, or an unreachable goal. The ORCA grant which I received from BYU has allowed me to do something that I love – study math at a more rigorous and in-depth level than traditional math courses allow for.

While I would have liked to have been able to discover some new, groundbreaking algorithm or method to allow people to test root-finding algorithms to commonly used applications like banking, medicine, and etc., I instead contributed to the general fund of knowledge by exposing a methodology that will not provide the desired results, and therefore should not receive anyone else’s time or attention as it relates to this problem. Further, the things we learned have helped us in other parts of our project.