Richard Barney and Jean-Françios S. Van Huele, Physics and Astronomy
In our increasingly data-driven society, the ability to transmit secure messages is more essential than ever. This ability allows economies to thrive and protects both personal and national security. In order to achieve this security, cryptographers have developed methods to encrypt data. One of the most successful of these methods is to use a secure key to encrypt and decrypt the sensitive data. This method has been very successful but it is still possible for outside agents to obtain the secure key and thereby access sensitive information.
New technology is emerging which uses quantum principles such as entanglement and superposition to allow for much more secure key sharing. Quantum key distribution schemes such as those proposed by Bennet and Brassard1 and Ekert2 are attractive because security is guaranteed by the laws of physics themselves. However, these schemes do not take into account the imperfections that arise in the necessary physical equipment. For this reason, many physical quantum key distribution schemes are somewhat susceptible to eavesdropping.
A possible solution to this problem is integrating quantum erasers into quantum key distribution schemes. The principle of quantum erasure was first discussed by Scully and Drühl3 in 1982. They showed that it is possible to erase information about a quantum system through entanglement. This could be useful in quantum key distribution if it could allow authorized parties to erase information that would be useful to an eavesdropper without scrambling the key that they are trying to share.
A consequence of quantum erasure is that it alters the degree to which a quantum object behaves as a wave or a particle. Quantum objects obey the principle of wave-particle duality. The more they behave as a wave the less they behave as a particle and vice versa. Complete particle behavior corresponds to complete available information about one of the quantum object’s observable and complete wave behavior corresponds to the total lack of available information about that observable.
In order to better understand how quantum erasure can affect wave-particle duality, we examined a quantum erasure scheme, shown in Figure 1. This scheme uses the Stern-Gerlach effect to both create and then erase path information for a beam of quantum objects passing through the magnets. The first magnet entangles the position of the quantum object with its spin. The second magnet does the same, but if it is oriented in a different direction than the first magnet, this second entanglement will erase some of the information the first magnet created. By varying the angle between the orientations of the two magnets, we can control how much path information is erased. This can be quantified by the quantum coherence of each quantum object as it exits the second magnet.
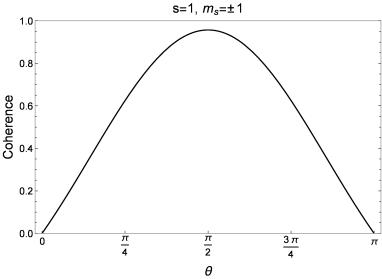
We found that the degree of coherence which can be recovered depends on the spin quantum numbers (s and ms) of the quantum objects and the angle between the orientations of the two magnets. Figure 2 shows the coherence recovered for spin-1/2 quantum objects. Both spin substates (ms=1/2 and ms=-1/2) recover full coherence when the magnets are oriented at an angle of π radians to each other.
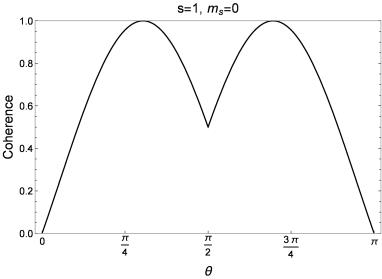
Figure 3 shows the coherence recovered for spin-1 quantum objects. In this case only one of the spin substates (ms=0) can recover full coherence. Instead of at 90°, this occurs approximately at the angles 0.955 and 2.186 radians. The other spin states can never recover full coherence regardless of the magnet orientations.
These results have implications for quantum key distribution schemes. If information is made available about a two-level quantum system, it is always possible to erase this information through a rotation. However, this is not guaranteed for systems with more than two levels, such as the spin-1 case in the Stern-Gerlach quantum eraser. These principles should be taken into consideration when designing any quantum key distribution scheme which makes use of quantum erasure.
Figure 1 – A quantum eraser using the Stern-Gerlach effect. Quantum objects are emitted from the source S. The first magnet M1 entangles the object’s spin with its position in z. The second magnet M2 entangles the object’s spin with its position in another direction. This erases some of the path information created by the first magnet. A set of self-interference patterns is observed on the detector screen D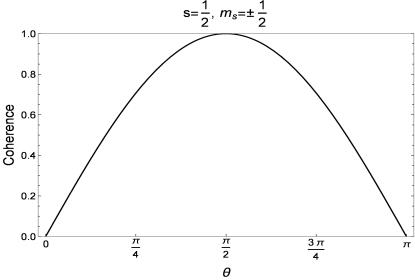
Figure 2 – Recovered coherence for spin-1/2 quantum objects
Figure 3 – Recovered coherence for spin-1 objects
1 C.H. Bennett and G. Brassard, “Quantum public key distribution,” IBM Technical Disclosure Bulletin 28, 31533163 (1985).
2 A.K. Ekert, Phys. Rev. Lett. 67, 661-663 (1991).
3 M.O. Scully, K. Drühl, Phys. Rev. A 25, 2208 (1982).