Michael Borden and Dr. Steven E. Benzley, Civil and Environmental Engineering

Three-dimensional finite element analysis (FEA) is an important design tool for scientists and engineers. Before the analysis can begin, a continuous domain must be subdivided into small elements (i.e., finite elements). The process of subdividing a continuous domain is called meshing. There is currently significant research being devoted to the generation of such meshes. Tetrahedral meshes are well developed and have been incorporated in numerous software packages. Hexahedral meshes provide some advantages over tetrahedral meshes but are currently more restrictive in the geometrical shapes they can fill.[1]

One method used to create three-dimensional meshes is sweeping. Sweeping consists of meshing a source surface of a body with a two-dimensional quadrilateral mesh and then sweeping the mesh through the body creating hexahedral elements one layer at a time until a target surface is reached (see Figure 1). Sweeping algorithms can accommodate non-planar, non-parallel source and target surfaces and variable cross-sectional areas[2] as well as multiple source and target surfaces.[3]

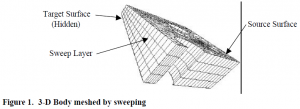
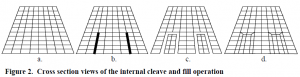
Currently, however, sweeping algorithms require that source and target surface meshes have the same connectivity. If a three-dimensional body is tapered from source to target surface, this requirement could lead to a wide variation in the density of the mesh, which may cause unacceptable error in the analysis. Figure 2a shows a cross-sectional view of such a body. To solve this problem, the internal cleave and fill algorithm has been developed and implemented into CUBIT, a finite element mesh generation software tool kit.
The internal cleave and fill algorithm proceeds through four steps:

1) Define a path within the mesh. For a path to be defined, the user of the software must specify the sweep layer, a number of intervals, and the direction in which the operation should be performed. Once all the information has been given the algorithm then finds all the nodes (a node is located at each vertex of a hexahedral element) contained in the specified layer and assigns a weight to each one. The weight of each node depends on its position within the body. All nodes that lie on a surface of the body are given a weight of zero and the weight increases in successive rings as the nodes approach the center of the body. Once the nodes have been weighted, the path is defined as the nodes with a weight equal to the number of intervals given by the user.
2) Define a sheet of nodes by projecting the path to a surface of the body. As the path is projected through the body, the nodes that it passes through are collected and used to define a cleaved sheet. The highlighted edges in Figure 2b show the cleaved sheet in the given body.
3) Create a cleaved volume. A cleaved volume is created by separating all the hexahedral elements that lie on the cleaved plane from the surrounding elements therefore creating a cleaved volume. A cleaved volume is shown in Figure 2c.
4) Fill the void between the cleaved volume and the existing mesh. This step is accomplished by a process known as pillowing.[4] Figure 2d shows the resulting mesh after the void has been filled with a “pillow” of hexahedral elements.

The internal cleave and fill method is very useful in allowing the modification of a traditionally created swept mesh. It can be easily incorporated into existing three-dimensional all hexahedral meshing schemes. High quality refined elements are a feature of this algorithm.

References

1. Benzley, S.E., Perry, E., Merkley, K., Clark, B., and Sjaardema, G., “A Comparison of All- Hexahedral and All-Tetrahedral Finite Element Meshes for Elastic and Elasto-Plastic Analysis,” Proceedings, 4th International Meshing Roundtable, Sandia National Laboratories, 95, pp. 179-191, October 1995.
2. Staten, M. L., Canann S. A., and Owen, S. J., “BMSweep: Locating Interior Nodes During Sweeping,” Proceedings, 7th International Meshing Roundtable 98, pp. 7-18, October 1998.
3. Mingua, L., and Benzley, S.E., “A Multiple Source and Target Sweeping Method for Generating All Hexahedral Finite Element Meshes,” Proceedings, 5th International Meshing Roundtable 96, pp. 217-225, October 1996.
4. Mitchell, S.A., and Tautges, T.J., “Pillowing doublets: refining a mesh to ensure that faces share at most on edge,” Proceedings, 4th International Meshing Roundtable 95, pp. 231-240, October 1995.