Rachel Gardner, Dr. Manuel Berrondo, and Dr. Jean-Francois Van Huele, Department of Physics and Astronomy

Introduction

The purpose of my research was to design and create a model for Quantum Energy Teleportation (QET) that maximizes the usefulness of the teleportation. The model allowed me to contrast QET to Quantum Information Teleportation (QIT), and in particular explore the attributes and limitations of QET. Specifically, I wanted to improve efficiency by minimizing the energy losses of the process and the intrinsic losses due to physical parameters and practical implementations. With the mentorship of Manuel Berrondo and Jean-Francois Van Huele, I created a model to analyze the state that maximizes this efficiency of the teleported energy, reduce these losses, and analyze the effects of QET’s model’s parameters.

Methodology

Quantum energy teleportation (QET) is a recent research topic that has caught the attention of the quantum information technology community. To precede my efforts in building a model for QET, I reviewed Hotta’s paper and began analyzing the parallels between QIT and QET, including the three fundamental steps: Entanglement, Measurement, and Transformation/Extraction. In addition to studying Hotta’s general QET model, I replicated Hotta’s calculations step by step to ensure understanding and a successful platform to build my own model. (See table for replication in Results). Hotta only published calculations for the ground state of his Hamiltonian and general model, so my mentors and I expanded the general model for all three excited states by using the alternative three eigenstates and eigenvalues in all of the calculations. Building upon Hotta’s replication and expanded model in Mathematica, I expanded his model from a two-parameter system to a four-parameter system, allowing for the original parameters h and k to be limited from both locations by expanding the parameters to ℎ𝑎, ℎ𝑏, 𝑘𝑎, and 𝑘𝑏. By altering the parameters in Hotta’s general system, I had to be cautious of the assumptions that Hotta had made. Because I expanded the dimensions sample space of my Hamiltonian, I could no longer assume the shortcuts of a two-dimensional Hamiltonian. Though my computer’s processing speed could handle a Mathematica algorithm for Hotta’s two-parameter system, when I expanded the model to my general four-parameter system, my computer struggled processing such high sample space. Not only were the calculations lengthy in time, the end results were lengthy in form. Mathematica could not handle the task of algebraically simplifying the complexity of the equations, so I decided to approach my understanding of QET by simplifying the method until the model essentially falls apart. I challenged the model to its simplest form. Rather than using my expanded model of a four-parameter Hamiltonian, I compressed Hotta’s model to only one parameter by making h=k. In this condenses model, I analyzed the results to ensure effectiveness of QET’s system.

Results/Discussion

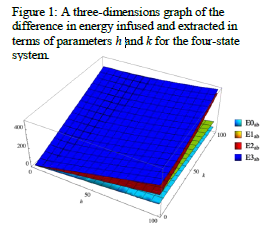
My mentors and I repeated the calculations of Hotta’s model to ensure its validity and also to understand the fundamentals and necessities of his model. Table 1 shows the calculations we acquired after replicating Hotta’s methods; it can be compared to Hotta’s publication as the same results. Upon replicating his theory, we expanded his model to the excited eigenstates of his Hamiltonian, where he strictly worked with the ground state. We analyzed the end results of the states, the energy extracted, and measured that ground state was the most efficient of the four model’s states. The efficiency of the model was defined by the smallest difference between the energy infused and the energy extracted from the system. Figure 1 demonstrates a three-dimensional graph of the energy difference in terms of the two parameters h and k; it can be observed that the ground state 𝐸0𝑎𝑏 has the least difference or the greatest efficiency of this four-state expanded model.

Having verified the validity of Hotta’s original model, we explored the effects of altering the model by extending it into a four-dimensional parameter system. Even though a four-parameter system is achievable, the processing speed of my computer and Mathematica’s lack of ability to simplify complex algebraic expression limited the research and analysis of this general model. Despite these limitations, I was able to verify that the model created was successful. After simplifying the algebraic expressions by hand for the eigenvalues and eigenvectors, the lowest eigenvalue simplified to zero, ground state, and the eigenvectors had a symmetry that paralleled with my precious four-state system. Another check consisted of checking the units on each variable: the eigenvalues and eigenvectors were unitless and the energies, infused and extracted, ended with a singular power of the parameters. These units were as expected.

My mentors and I simplified the two-parameter model to a one-parameter system to test the limitations of QET. Simplifying the Hamiltonian by setting h=k allowed us to review the symmetry of the eigenvalues and eigenvectors as wells as the efficiency of the system. Each variable, similar to the four-parameter model, simplify to the correct units. Table 2 illustrates the values of the simplified model. Figure 2 demonstrates a graph of the energy difference in terms of the parameter h for four eigenstates of the simplified model.

Conclusion

After analyzing the results of three models of QET, we have concluded that the most efficient state is the ground state of each Hamiltonian system. It can be observed from Figure 1 and Figure 2 the state that minimized the losses producing the most efficiency is always the ground state. Each system has a parallel symmetry in the eigenvalues and eigenstates. Further research would include working on simplifying the algebraic expressions for the four-parameter system and possibly extending a general model to more parameters.