Emily Menden and Dr. Sean Warnick, Department of Computer Science
Introduction
The area of quantitative ecology has been growing in recent years as biologists and mathematicians come together to better understand the ecological dynamics in the systems that surround us. One category of systems that begs to be studied is systems in which species are considered for elimination from or introduction to the system. For example, scientists have been debating for years whether or not to eliminate the malaria-‐carrying species of mosquitos. To put the situation in perspective, there are about 3,500 species of mosquito and only 30-‐40 of them carry malaria. One solution to eliminate malaria is to get rid of the species that transmit the disease; one problem with this solution is we do not understand the consequences of those actions.
Consequently, Yellowstone National Park is a prime system to study when considering the issue of species elimination and introduction. In the 1920s and 30s, wolves were extirpated from Yellowstone because of the economic trouble they were causing ranchers and their cattle. In the winters of 1995 and 1996, wolves were reintroduced to Yellowstone, starting what is understood today as a trophic cascade. A trophic cascade occurs when an apex predator is introduced or eliminated from an ecosystem; it is characterized by the release or suppression of herbivores which affect the growing rates of primary producers. In the case of Yellowstone, the introduction of wolves caused elk populations and behaviors to change allowing woody browse species to increase. This release from herbivory had many other ecological impacts, such as the increase in beaver populations. In this study, I set out to computationally model this trophic cascade as a start in computationally understanding the problem of species elimination and introduction.
Methodology
It has been suggested by several scientists that the trophic cascade in Yellowstone National Park is characterized by changes in elk population levels and in their behaviors. After thoroughly researching what work has been done in Yellowstone, I proposed to create a computational model of both the population and behavioral dynamics since wolf reintroduction.
To model population dynamics, I used a variation on the classic Lotka-‐Volterra equations which are a set of differential equations used to model competition in animals. In this study, the population dynamics between large animals such as elk, wolves and bears were studied. Data were taken from the published reports of Yellowstone National Park and through the synthesis of many published papers on the subject. I anticipated including other animals in the analysis of the system, however there were some limiting factors disallowing me to do so. The largest factor being lack of data collected and published on the animals. To model behavioral dynamics, I anticipated adapting commonly used pursuit evasion game algorithms to the behavior patterns of the elk and wolves in Yellowstone. The classic pursuit evasion game is a model of the behavior of a predator chasing its prey. In the case of Yellowstone, there is short-‐term and long-‐term behavior changes that have occurred as a result of wolf reintroduction. The successes and failures of my methods will be discussed in the next section.
Results
I studied a few models in my research period. One model (Model 1) is the classic Lotka-‐Volterra equations applied to only wolves and elk. Wolves and elk are believed to be the greatest contributors and controllers of the trophic cascade so a close study of their relationship is absolutely necessary. Another model (Model 2) studies the relationships between the wolf-‐ elk-‐bear system in Yellowstone. The reason for the study of this system is the shift in bears’ carnivorous diet since the 1990s. Discussion on this model and its usefulness is presented below. I will also report on how behavior dynamics of the wolves and elk are modeled.
Model 1
The set of equations used to characterize the predator-‐prey relationship between wolves and elk were as follows:
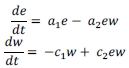
Where e represents the number of elk at a given time, w represents the number of wolves at a given time, 𝑎’ is the density-‐independent growth intrinsic rate of the prey population in the absence of predators, 𝑎) is the constant predation rate (fraction of the prey population eaten per predator), 𝑐’ is a constant per capita mortality rate of predators, 𝑐) = k𝑎) where k is a constant conversion rate of eaten prey into new predator abundance.
Through data analysis and hypothetical estimation, the parameters described above were found to be
![]()
The results of this simulation correlate reasonably well with the numbers of elk and wolves published by Yellowstone. This model is sensitive to perturbation in the parameters. This means that changing the parameters even slightly could yield results which are not in strong accordance with the data published of the Yellowstone animals. Because of this sensitivity, I explored another model, with the hypothesis that it could better explain the system.
Model 2
In this second model, I analyzed the relationship between wolves, elk and bears. The reason for including bears was because it has been observed that since the 1990s, bears have shifted their carnivorous diet from trout to elk calves. The reason for this shift in diet is the unintended introduction of a non-‐native species of trout into Yellowstone waters. The non-‐native species have out-‐competed the native species and they live too deep for the bears to reach them.
As a result, bears have shifted their diet to elk calves. This shift in diet has had little impact on the bear population, however, it could be impacting the population growth of the elk.
The set of equations used to characterize the wolf-‐elk-‐bear system is below:
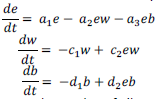
Where, similar to Model 1, e represents the number of elk at a given time, w represents the number of wolves at a given time, 𝑎’ is the density-‐independent growth intrinsic rate of the prey population in the absence of predators, 𝑎) is the constant predation rate (fraction of the prey population eaten per predator), 𝑎5 is the constant predation rate (fraction of the prey population eaten per predator), 𝑐’ is a constant per capita mortality rate of predators, 𝑐) = k𝑎) where k is a constant conversion rate of eaten prey into new predator abundance. 𝑑’ and 𝑑) represent the same constants as c, pertaining to the bear population.
Through data analysis and hypothetical estimation, the parameters described above were found to be
![]()
Like Model 1, these results correlate reasonably well with the data published on these animal populations in Yellowstone. Also similar to Model 1, this model is sensitive to perturbations. This model was created with the hypothesis that it would be more robust because it considers more factors (i.e. bear populations) than Model 1.
Behavior Dynamics
During the course of this project, I began modelling the behavioral relationships between wolves and elk. One initial hypothesis was to use pursuit-‐evasion games to model the active hunting and chasing between wolves and elk. While this is certainly a dynamic among these animals, there are long-‐term dynamics that should be considered as well. For example, wolf pack territory-‐shifts and elk migration patterns may have changed over time. These are not changes that were viewed over-‐night but have been studied over several years. With both short and long-‐term dynamics at play, I needed to have a way to model behavior over short and long periods of time.
To model the behavioral dynamics of the large mammals of Yellowstone, I am using a simulation application called NetLogo. It allows for modeling short and long-‐term dynamics. Thus, I am able to model pursuit and evasion as well as migration patterns of elk and territory shifts of wolf packs.
Conclusion
As of right now, the effects of species elimination and introduction are not well known or predictable. This research is being done in an effort to better understand the potential impacts of species elimination and introduction. I chose to study this issue in Yellowstone National Park because the ecosystem is somewhat closed, making inputs and outputs of the system easier to identify. In the future, I hope to use this work to study broader, more open systems where species elimination or introduction is a serious consideration. The work presented here as well as other results were presented at the Student Research Conference in the College of Physical and Mathematical Science, Brigham Young University. I am in the process of writing an Honors thesis on this research.
