Michael Greenburg and Dr. Steven Turley, Department of Physics and Astronomy

Introduction

The effects of small surface irregularities on a mirror’s reflectivity are fairly easy to calculate, but roughness on the same order of size as the wavelength of incident light disallows the use of some simplifying approximations. As a result, the effects of such roughness on reflectivity are not well understood. I enhanced an existing program that calculates the surface current induced by an incident plane wave on a conducting surface of arbitrary shape, thereby allowing reflectance as a function of angle to be determined.

Methodology

Calculating the surface current induced by an incident electromagnetic wave without using simplifying approximations involves an integral equation without an analytical solution—the current lies within the integral and can only be extracted with numerical methods. One must discretize the problem to solve it, leaving a matrix-vector equation. Such an equation scales as n2 in space and n2log(n) in time—a surface with 1000 points takes four times as much memory and over four times as much time to solve for as does a surface with 500 points.

A program to solve for induced current was written in Fortran due to its speed and the availability of extensive linear algebra libraries for it. I inherited the program, which at the time was able to run on a single processor and calculate reflectance for flat mirrors with or without random roughness. I expanded its capabilities, and it can now accept many more types of surfaces (including focusing mirrors and gratings), complete multiple simulations in one program run, set parameters such as surface type and length based on configuration text files (rather than recompiling when parameters change), and utilize as many processors as are available. The program was tested and found to reach results consistent with analytical solutions for simple surfaces.

Results

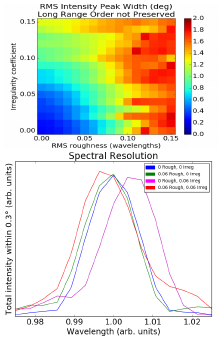
Roughness on diffraction gratings is even less well understood than on flat mirrors, so I built diffraction gratings with random bumps and divots and with slight inconsistencies in grating spacing. The degree of grating spacing inconsistency and the size of bumps and divots could be varied. Varying both yielded the expected results— peak width increased as roughness and spacing inconsistency increased (see figure 1).

Spectral resolution, a measure of how well a diffraction grating filters light by wavelength, was somewhat harder to measure due to the memory limits inherent to running computations on desktop computers. As the illuminated area of a diffraction grating increases, the range of angles across which reflected light of a given wavelength is scattered narrows. The surfaces which I tested were about 1000 wavelengths long— less than 1 mm for visible light. This meant that the broadening of reflectance peaks due to small surface size drowned out the effects of roughness and surface inconsistency on spectral resolution (see figure 2). For this reason, much larger simulations will be needed to determine the true effect of grating imperfections on spectral resolution.

Discussion

A supercomputer will be required to accurately determine how much the spectral resolution of a diffraction grating is affected by different types of surface imperfections. To this end, I have modified the program to use MPI (an interface to allow information to be passed between processes) to allow parallel computation without shared memory. With this added functionality, the program can run on a supercomputer.

The program I have run thus far uses a 1-D surface (one slice of a real surface). In order to confirm our assumption that this gives accurate results, I will finish a similar program that uses a 2-D surface (which is as yet incomplete). Since such a surface requires much more memory than a 1-D surface, I will need to use the supercomputer even for seemingly modest computations. With my newfound expertise with MPI and the underpinnings of the 1-D program, I expect to finish the 2-D program in short order.

Conclusion

Although the classification of the effects of grating imperfections on reflectivity is valuable in itself, a large part of the utility of the program I have modified and polished lies in its versatility. Upon confirming that the results given by the 1-D program are consistent with those given by the 2-D program (we assume a constant scaling factor to be the only difference), we can confidently proceed to classify the effects of irregularities on many types of surface with great accuracy due to the massive amount of memory afforded by the supercomputer.