Garett Brown and Dr. Manuel Berrondo, Department of Physics and Astronomy

Introduction

The complexity and pattern found in animal aggregations, such as starling murmurations, reveals emergent phenomena which arise from the simple, individual interactions of its members. Whether the animal aggregation is the result of a group of birds, a group of fish, or a collection of insects, we consider all types of animal aggregations to be some form of ‘flocking.’

Shortly before the 1990s, C. Reynolds developed a computational model to simulate the motion of a flock of birds. He coined the term “boid” as a shortened term for bird-oid, which is essentially a self-propelled particle that imitates the behavior of a bird. His model was based upon an averaging of spatial nearest-neighbor velocities. Later work was developed by T. Viscek who also built upon spatial nearest-neighbor averaging. While these models have their qualities, their lack of spontaneous dynamics questions whether they capture the true emergence found in flocking behavior.

Our attempt to create emergent behavior has been to begin with a reductionist approach (creating rules that regulate a system of ‘particles’ which interact with each other to produce a wholly different set of emergent properties) in addition to using holistic tools to analyze the results.

Methodology

Simulated in two-dimensions, our model shows that self-driven particles (boids) group together and display emergent flocking characteristics. Thus, rather than considering the flocking behavior that our model simulates to be literal, we consider the animations as a projection from three-dimensional space into two-dimensional space. The model is based on the ideas of consensus and frustration. Consensus is a nonlinear, novel, democratic, non-reciprocal, nearest topological-neighbor averaging that drives the boids toward one of three unique phases—aligned, clockwise, and counterclockwise. Frustration is a perturbation that essentially breaks the symmetry of the flock and damps out excessive consensus—pushing the boids beyond these simple phases and toward disordered behavior. The nonlinearity merged with the perturbation produces characteristics which go beyond the dynamic interplay of global and local phase transitions. The interplay between these two forces is akin to the biological battle of maintaining a homeostasis state that is found in nature.

Results

The dynamic interplay of phases and phase transitions is the heart of emergence in our model. Phases and phase transitions alone do not produce emergent flocking behavior. The behavior resulting from a single phase transition does not possess the dynamics that are present in the long term behavior of flocks. Thus, the continuous interplay between the three unique phases of our model create time dependent variations in flocking behavior. Without these shifts between phases, flocking phenomena would not emerge from the simple interactions of the boids.

The competing forces of consensus and frustration produce a system whose behavior is perhaps totally unexplainable by the simple rules and boid-boid interactions. During the course of a single simulation, a flock may stay tightly bound the entire time, or it may spread out to fill the entire space the entire time, or it may transition back and forth spontaneously between being tightly bound and filling the space.

It would be absurd to believe that still frames or screenshots could adequately capture the dynamic evolution of the animated simulations of our model, even so, the Fig. 1 is a sample of the flocking that our model produces. It is most important to note how emergent behavior is the dynamic interplay of the three unique phases that arise from pure consensus. It becomes clear that both the shape and evolution of the frustrated flock are complex and active. Thus, phase transitions are the essential building blocks of emergent flocking behavior; however, they are insufficient in and of themselves to produce a truly emergent flocking phenomenon.

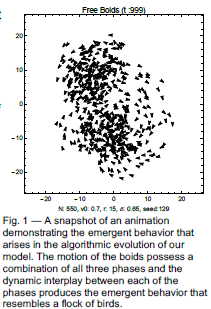
Discussion and Conclusion

Models possess utility that allow for the prediction of results. However, simply because a model predicts results correctly, does not inherently mean the model is ‘correct.’ Our novel approach to modeling emergent flocking has proven to be robust and versatile; even so, our use of topological nearest neighbor interactions rather than spatially dependent nearest neighbor interactions seems counterintuitive. Surprisingly, comparisons of topological neighbors and turning radii between our model and the observations of European starlings (Sturnus vulgaris) made by A. Cavagna and his group in Rome, Italy reveal our model to have remarkable accuracy and physical realism.