Tyler Bahr and Dr. Mark Transtrum, Department of Physics and Astronomy
Introduction
The foundational model of voltage spiking in neurons, formulated by Hodgkin and Huxley in 1952, is composed of 4 dynamical variables and 25 parameters. The sheer complexity of the basic neuron model is a key issue which makes neural simulations computationally expensive. We performed a parameter identifiability analysis of the Hodgkin-Huxley (HH) model and found that around half of the parameters are unnecessary. Using the Manifold Boundary Approximation Method (MBAM), an information-theory based approach to model reduction, we derived a simpler model of spike firing in response to a smooth pulse input with only 3 dynamical variables and 14 parameters. Preliminary results indicate that the reduced model retains much of the original HH model’s predictive power. Next, to evaluate the accuracy of our reduced model, we observed the behavior of a single reduced model neuron under various simulated experimental conditions and compared it with the behavior of the original HH model neuron. Second, we constructed networks of these reduced neurons and compared their behavior with homologous HH networks. Finally, we conducted a preliminary exploration of model reduction using MBAM on networks.
Materials and Methods
Recent advances combining information theory and differential geometry have led to new methods of removing unnecessary parameters from models. The Manifold Boundary Approximation Method (MBAM) makes structural approximations to a model by identifying the boundary of a “Model Manifold” embedded in prediction or data space. We used the MBAM to identify and remove 11 parameter combinations from a 25-parameter Hodgkin Huxley model, bringing the current total to 14 tunable parameters.
Model behavior for a single neuron was evaluated by running simulations for various experimental paradigms. This mainly included changing parameter values and input currents. To evaluate network behavior, we constructed connectivity maps using matrices. Each row in the matrix represent a neuron conveying a signal, and each column represented a neuron receiving a signal. Thus, each entry in the matrix represented a synaptic connection. For simplicity’s sake, we used gap junction synapses- simple connections in which the applied current to the receiving neuron is a function of the voltage difference between the two.
Because emergent network behavior is usually found in neurotransmitter networks with time delays, we attempted to construct a network model with a time delay, however we ultimately found that our computational tools were unable to solve the differential equations when a time delay was included.

Results
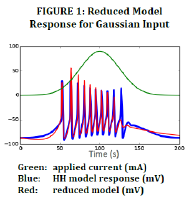
Our evaluation found that the 14-parameter model was excellent for reproducing behavior with parameter values within 10% of the original values (data not shown here), and that it was excellent for both smooth and steady input currents. Interestingly, sharp changes in input current resulted in exaggerated neuron response as exemplified in a step current input function (Figure 2). In neuron networks, input current is also constantly changing and sharply, so this approximation became a clear issue affecting spike amplitude in networks (Figure 3).
As predicted, we also found that the combinations of parameters in our reduced model had physical significance relevant to neural spike firing, like ion currents and voltage thresholds.
Discussion
MBAM model reduction eliminates model attributes that are not employed in the set of predictions it is designed to reproduce. Because we chose a gaussian input current, which that increases and then decreases smoothly, our reduced model captured voltage threshold and firing rate effectively, but failed to capture a correct response to sharp changes in input. Theoretically, if the process of model reduction were to be repeated with a different input such as a sawtooth wave, square wave, or high-frequency sine wave, the reduced model might capture these sharp changes in input more accurately.
Another major outcome of this project was the derivation of an entire class of neuron models. The 14-parameter model is only one of 8 different models of varying complexity that we produced using our model reduction methods.
Conclusion
A great obstacle faced by the neuroscience community is the sheer complexity of neurological models. Simplified neuron models exist, but they fail to capture key characteristics of true neuronal behavior and none has parameters that can be connected to real physical quantities. In this project, we have developed (and evaluated) a set of novel neuron models derived using methods previously unknown to the field of Neuroscience. By evaluating the drawbacks of our model, we have also identified key points for choosing experimental conditions before future attempts at model reduction in neuron models. Our work will help make modeling the brain easier in the future.