Joshua Frei and Dr. David Lignell, Chemical Engineering Department
The whorls and vortices of smoke plumes, churning waterfalls, and crashing waves have a captivating sense of mystery about them. This chaotic, seemingly random fluid motion is known as turbulent flow, and it is ubiquitous both in day-to-day life and in engineering problems. Despite the many advances in technology, much of turbulence remains a mystery. It has been called the most important unsolved problem in physics [1].
The problem with turbulence is not a lack of understanding of the laws that govern its behavior, rather it is the complexity of describing those laws that presents the challenge [2]. The Navier- Stokes equations dictate the laws of turbulent flow, but it takes millions of computer hours to solve this problem on a domain any larger than a few cubic centimeters. A model that is accurate, yet computationally inexpensive is in high demand.
Many models exist to solve the turbulence problem. One of these, DNS (Direct Numerical Simulation), provides a full numerical solution to the Navier-Stokes equations. Unfortunately, it is the most expensive model computationally. LES (Large Eddy Simulation) provides an accurate solution by resolving large scale turbulent eddies, and by modeling the smaller eddies. While it is less expensive than DNS, it is still relatively costly. Another model, known as RANS (Reynolds Average Navier-Stokes), is widely used in engineering applications. It is accurate, and less expensive than LES, but it is problematic in modeling non-linear effects present in heat and mass transport and chemical reactions. Still another model is called ODT (One-dimensional Turbulence). This model views a fluid domain along a one-dimensional line of sight, and then subjects the domain to a series of turbulent eddy events. While it is limited to only one dimension, ODT can be extended to three dimensions using ODTLES (Onedimensional Turbulence Large Eddy Simulation). This model has also proven to be accurate, and is less expensive computationally.
These and a host of other models have been applied to a variety of turbulent flow situations. One particularly interesting case is high Schmidt number flow. The Schmidt number is the ratio of kinematic viscosity to molecular diffusivity. It compares the rate at which momentum is transferred by turbulent eddies to the rate at which molecular species diffuse throughout the fluid medium. A Schmidt number of one represents equivalent momentum and molecular diffusivities. Low Schmidt number flow means that a species diffuses much faster than turbulence mixes the fluid. The most interesting case is high Schmidt number flow, which means that turbulent eddies propagate through the fluid much faster than molecular diffusion can occur. This results in many fine scale concentration gradients throughout the fluid. Such a flow regime occurs when the scalar species in a fluid has an extremely low molecular diffusivity. High Schmidt number flow is common in combustion because of the low molecular diffusivity of soot particles. The wide range of length scales present in high Schmidt number flow makes it very difficult to model.
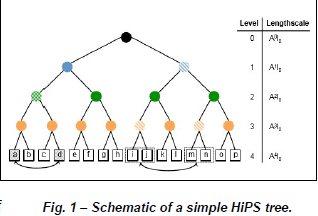
The new Hierarchical Parcel-Swapping method (HiPS) developed by Kerstein [3,4] is well suited for the job of modeling high Schmidt number flow. The model is structured as a binary tree, with parcels at the base of the tree that contain the fluid properties. Each level of the tree has a specific length and time scale. Turbulence is simulated by randomly swapping the levels of the tree. This swapping is governed by a Poisson distribution based on the length and time scales of each tree level. The parcels at the base of the tree are then mixed by instantaneously averaging their properties, or by using more complex rate-mixing equations. The many length scales of the tree make it well-suited for handling the many length scales present in high Schmidt number flow.
My mentor, Dr. David Lignell, an expert in stochastic turbulent modeling, extended his existing ODT framework code to include a HiPS model. My primary contribution came in the implementation of variable Schmidt numbers to the HiPS framework. Throughout the semester, I met with Dr. Lignell and other students in our research group to discuss HiPS and variable Schmidt number flow. The first step was to summarize the length and time scales of the tree in terms of the tree level (i) the initial length scale (L0) and the initial time scale (τ0). We then determined Schmidt numbers at each level of the tree. The Schmidt number can be defined by the square of the ratio of the Komolgorov length scale to the Batchelor length scale. The Komolgorov scale represents the turbulent eddies, and the Batchelor scale represents the molecular diffusivity. In high Schmidt number flow, the Batchelor scale is smaller than the Komolgorov scale. We assumed the Batchelor scale to reside at the base of the tree, which allows the Schmidt number to vary based on the level of the tree in which the Komolgorov scale resides. The Schmidt number in HiPS therefore becomes a function of the number of levels in the tree (N), and the index of the Komolgorov tree level.
To implement high Schmidt number flow in HiPS, the swapping rate for all parcels below the Komolgorov length scale must be governed by the Komolgorov time scale. This slows down the mixing rate at the lower levels of the tree, creating the steep concentration gradients characteristic of high Schmidt number flow. The HiPS structure creates a notable limitation on the Schmidt numbers that can be implemented in the model. Its binary nature constrains the Schmidt number to powers of 4 (i.e. Sc = 1, 4, 16, 64, etc.). Additionally, because of the tree structure, a swap of parcels at any level of the tree is dependent upon the time scale of its grandparent node, which requires the Komolgorov time scale to be implemented two tree levels higher than the Komolgorov length scale. This culminates in the equation i*=(N-1)-log4Sc, where i* represents the level at which the Komolgorov time scale is implemented, N is the number of levels in the tree, and Sc is the Schmidt number.
After completing the implementation of high Schmidt number flow cases in the HiPS framework, our group is now in the validation stage. One group member ran a HiPS simulation for a chemical reaction case using Sc = 1, 4, 16, 64, and 256 and graphed the selectivity of the reaction. These graphs will be compared to Frankel, McMurtry, and Givi’s [5] results on selectivity for variable Schmidt numbers to see if they exhibit the same trend. Additional validation will be conducted by comparing base parcels of a N = 8, Sc = 1 tree to a N = 10, Sc = 16 tree. The base parcels of the smaller, unity Sc tree should be close in value to groups of 4 parcels in the larger, Sc = 16 tree. We will verify our results further by graphing the energy spectra of our results and watching for the characteristic -5/3 slope. By comparing selectivity graphs, base parcels for varying Sc cases, and the energy spectra, we hope to validate our model. It can then be applied to additional cases.
In addition to the implementation of high Schmidt numbers to the HiPS framework, I conducted a literature review on the topic of high Schmidt number flow modeling. The combination of the code implementation and the literature review has promising content for publication in an academic journal and for presentation at an academic conference. This has been a valuable learning experience for me, and I look forward to carrying the project through this upcoming semester. Thank you for this opportunity.
References
1. Feynman R., Leighton R. B., Sands M. (1964) The Feynman lectures on physics (Addison- Wesley, Boston, MA).
2. Durbin PA. 2011. Statistical theory and modeling for turbulent flow. 2nd ed. ed. Wiley, Chichester, West Sussex, U.K.
3. Kerstein A. 2013. Hierarchical parcel-swapping representation of turbulent mixing. part 1. formulation and scaling properties. Journal of Statistical Physics 153(1):142-61.
4. Kerstein A. 2013. Hierarchical parcel-swapping representation of turbulent mixing. part 1. formulation and scaling properties. Journal of Statistical Physics 153(1):142-61.
5. Frankel S.H., McMurtry P.A., Givi P. 1995. Linear eddy modeling of reactant conversion and selectivity in turbulent flows. AIChE J. 41(2):258-66.