Justin Ward and Dr. David Lignell, Chemical Engineering Department
Introduction
The purpose of this project is to address the unmet need for a comprehensive, multiscale, regime- and fuel-independent turbulent reacting model by using a novel, physics-based strategy called Hierarchal Parcel Swapping (HiPS). Turbulent flow has been called the most important unsolved problem of classical physics. Modeling turbulent flow is extremely important due to the fact that nearly all flows in the real world are turbulent. Though the exact details of turbulent flow are not of great importance to an engineer, the effect turbulence has on chemical reactions and the overall chemical properties is vital. The solution to the turbulence problem is obtained through models and simulations. The current issues facing turbulence modeling is that the simulations are too computationally costly or do not provide adequate resolution.
The most widely used model for turbulence is RANS (Reynolds-Averaged Navier Stokes), which only solves for average properties of the fluid. The limitation of this model is that it is unable to model the fluctuating non-linear effects that are present in chemically-reacting flows. Direct simulations that resolve all turbulent motion cost millions of CPU hours for very small domains. The proposed HiPS model has the capability in conjunction with other models to provide adequate resolution and not be computationally costly.
Methodology
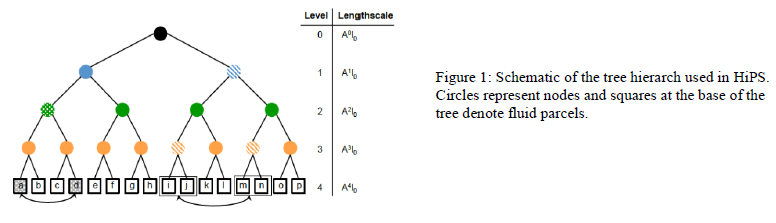
The computational cost of modeling turbulence increases with Reynolds number (Re) to the third power, where the Reynolds number describes how turbulent a fluid flow is. A larger Reynolds number requires higher resolutions and increased costs. The HiPS model involves a binary tree structure with levels that represents the turbulent scales (Figure 1). Nodes at the base of the tree represent notional fluid parcels whose chemical composition and other properties constitute the system state. Pairwise exchanges of the locations of individual parcels or subtrees (parcel groups) with frequencies dependent on subtree size emulate the inertial-range dependence of turbulent time scales on turbulent length scales. Fluid parcels are mixed according to a stochastic Poisson Process. The higher levels mix more frequently than the lower levels. The swapping rates are defined to be consistent to turbulent scaling laws.
The model was built using Python, and the simulations were run on the Fulton Super Computer. The HiPS code had previously been built to model turbulent non-reacting flow, and the code was extended to turbulent reacting flow. A simple two-step mechanism was chosen for running turbulent reacting flow simulations, where R is the desired product and P is the undesired product.
𝐴+𝐵→𝑅
𝐴+𝑅→𝑃
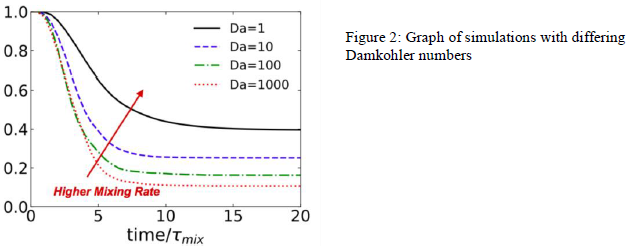
The reactions were simulated with differing Damkohler numbers to see if the simulations represent what physically happens in a reacting flow. The Domkohler number is a ratio of reaction rate to mixing rate. Higher Damkohler numbers represent higher reaction rates, and lower mixing rates. The condition of the simulations is mixing two separate streams. One stream is pure chemical A, and the other stream is pure chemical B. The simulations were run until equilibrium was reached.
Results and Conclusions
The simulations were run using a Reynolds number of 64, and using 9 levels. Figure 2 shows a graph of the selectivity of product R with differing Damkohler numbers. Selectivity is a measure of production of desired product R and undesired product P. Higher selectivity reflects more production of R and less production of P. The results show that lower Damkohler numbers (higher mixing rates) favor the desired product R. This is due to the fact that higher mixing rates reduces the local concentrations of product R, therefore reducing the production of product P. The results of the simulations are significant because they reflect what would physically happen with a similar reaction.
HiPS has a future within turbulent flow modeling. HiPS has proved through this study that it can reduce computational cost, but still provide physically meaningful results. The future of HiPS includes being combined with other turbulent flow models, and, eventually, applied to model combustion.