Jacob Badger and Dr. Larry Howell, Mechanical Engineering Department

Introduction

The purpose of my research was to explore the application of curved folding in designing rigid-foldable deployable mechanisms. In recent years, origami fold patterns known as “flashers” have been investigated for their ability to efficiently pack deployable surfaces. While many patterns have been investigated, none are capable of folding surfaces composed of rigid panels that bend only along crease lines. We hoped to identify one such rigid-foldable flasher by basing it on a curved-fold pattern known as a logarithmic spiral flasher.

Background

Curved folding is a form of origami where paper is folded along curves instead of straight lines, requiring that paper bend around creases. The surfaces formed by curved folding are known as developable surfaces (surfaces that can be flattened without tearing or stretching), and have the property that at every point on the surface there is at least one direction in which the surface is entirely flat. The lines that correspond to these flat directions are known as rulings. These rulings have been shown to have a strong correlation to straight-fold origami and algorithms have been proposed to discretize curved-fold surfaces into straight-fold origami patterns along these rulings [Lang et al. 17].

Our approach was to discretize the logarithmic spiral flasher along its rulings to obtain a rigid-foldable flasher pattern. We determined that the discretized pattern was not rigidly foldable, but this process led to a further investigation of two classes of curved folds known as ruling-rigid and smooth fold patterns. Ruling-rigid foldable curved creases require that both creases and rulings stay completely fixed within the paper throughout the entire folding motion. In contrast, smooth-foldable curved creases only require that creases stay fixed, allowing rulings to move freely throughout the folding motion. We determined the logarithmic spiral flasher to be smooth foldable. The remainder of our work was focused on developing the tools necessary to analyze smooth-foldable curved creases.

Results

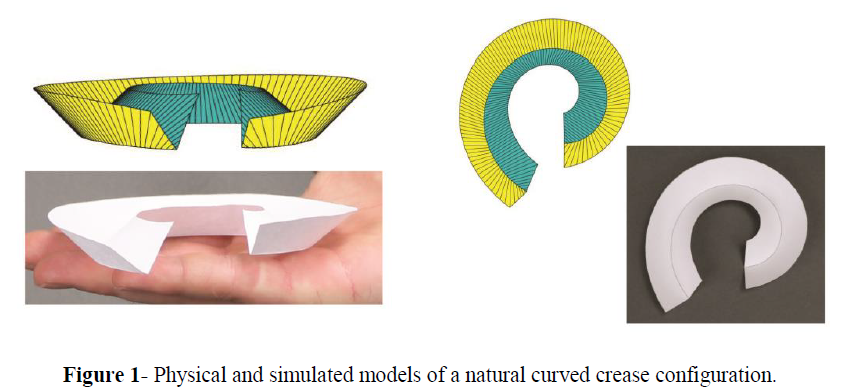
Relatively little work has been done to analyze smooth-foldable creases due to the complexity in modeling and constraining fold surfaces. As a smooth foldable crease is folded, the quantities usually used to parameterize fold surfaces change drastically. To Figure 1- Physical and simulated models of a natural curved crease configuration. simplify these complex relationships, we derived an alternative parameterization of curved folds known as normalized coordinate equations. These normalized coordinate equations relate curved fold properties to characteristics of developable fold surfaces and greatly simplify curved fold calculations.

Using this simplified form, we developed an energy method to predict the natural state of a general curved crease. One such natural fold configuration is shown in We applied this energy method to obtain a few surprising results.

We found the natural configuration of a general curved fold while close, is not necessarily a planar, uniform fold as first conjectured by Fuchs and Tabachnikov [Fuchs and Tabachnikov 99]. This result contradicts an assumption held for nearly 20 years, and helps to explain the erratic behavior of crease patterns like the Bauhaus concentric circle fold pattern. In addition, we found that the natural configuration of a quarter-circular crease, while neither planar nor uniform, appears to be ruling-rigid foldable. This result suggests that there is an energy cost involved in moving rulings within a fold surface, but verifying this result is left to future work.

Conclusion

The results of our research have been submitted to the 7OSME conference at Oxford University. In the future we plan to investigate properties of natural fold configurations and extend energy methods to multiple-crease patterns.

Sources

[Fuchs and Tabachnikov 99] Dmitry Fuchs and Serge Tabachnikov. “More on Paperfold-ing.” The American Mathematical Monthly 106:1 (1999), 27–35.

[Lang et al. 17] RJ Lang, TG Nelson, SP Magleby, and LL Howell. “Kinematics and Discretization of Curved Fold Mechanisms.” In ASME 2017 IDETC/CIE, IDETC2017-59747. ASME, 2017.