David W. Kastner and Dr. Steven L. Castle Department of Chemistry and Biochemistry

Introduction
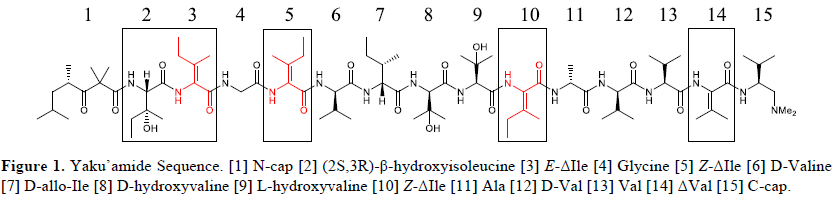
Yaku’amide A (YA) was isolated in late 2010 from the deep-sea sponge Ceratopsion sp. and exhibits
potent inhibitory activity against 39 human cancer cell lines via a potentially novel mode of action. ¹
However, due to its complex amino acid profile (Figure 1), which features unsymmetrical amino acids E
and Z-α,β-dehydroisoleucine (ΔIle), the total synthesis requires many steps and produces low yields. ² In
this study, we propose two synthetically simpler YA mimics that may retain its anticancer properties. The
proposed analogues were determined via molecular mechanics/quantum mechanics (QM/MM) hybrid
calculations and were selected from among eight sequences that replace ΔIle with either
dehydroethylnorvaline (ΔEnv) or dehydrovaline (ΔVal). The identification of YA analogues will greatly
increase synthetic output, making YA accessible to future anticancer research.

Methodology
Yaku’amide Model System Setup. There currently exists no crystallographic structure of YA and therefore
conformational searching was used to identify an initial structure for refinement. The RESP partial charges
for the MM calculations were computed using the RESP ESP charge Derive (R.E.D.) protocol ³ for all
nonstandard residues.To complete the MM function, missing bond stretch, angle bend, and torsion angle
parameters were identified using AmberTools paramchk and appended to the AMBER96 force field. ⁴
The input structures for the ONIOM(DFT:MM) calculations were prepared and optimized with AMBER.
All analogues and YA converged to the same secondary structure.
ONIOM(DFT:MM) Hybrid Calculations. Further optimization of YA and the analogues was performed
using the ONIOM method ⁵ as implemented by Gaussian 09. ⁶ Calculations were set up such that the QMMM
boundary divided the Cα-N and Cα-C bonds to avoid partitioning of peptide bonds and valences were
satisfied with the default method. 2Three different ONIOM layer combinations were computed for YA
and the analogues. AMBER was used at the low layer in all calculations and the high layer was computed
with either B3LYP/d95(d,p), B3LYP/6-311g(d,p), or M06-2X/6-31+G(d) level of theory. ⁷
RMSD Calculation Setup. Either the entire structure or the backbone plus the QM region of each analogue
was superimposed with a structure of YA that was optimized with the same level of theory using the VMD
RMSD tool. Since RMSD calculations require that both structures have the same number of atoms, the
methyl groups of ΔEnv and (E) and (Z)-ΔIle were removed prior to the RMSD calculation.
Results and Discussion
RMSD Calculations. The first RMSD calculation used complete optimized structures to capture changes
in sidechain positioning. The second RMSD calculations used the backbone plus the QM layer, which
included the four ΔAAs, to identify the analogue with the fewest deviations to the backbone dihedrals
(Figure 2A). Furthermore, the two methods agreed and show the best retention of YA’s conformation with
the substitutions ΔEnv, ΔVal, and ΔVal at positions [3], [5], and [10] respectively. This analogue showed
the lowest predicted RMSD across all methods and basis sets (Figure 2B). The second-best combination
incorporated ΔVal, ΔEnv, and ΔVal at positions [3], [5], and [10] respectively. Moreover, it appears that
ΔEnv is a good candidate for conservation of dihedral angles of ΔIle but increased displacement of
neighboring sidechains. Thus, the ideal analogue should use an optimized combination of ΔVal and ΔEnv.

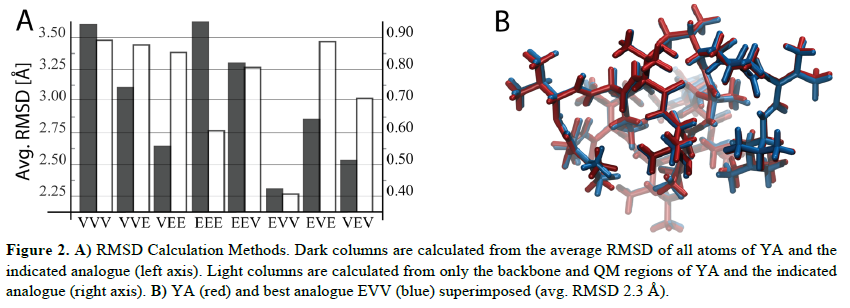
Figure 2. A) RMSD Calculation Methods. Dark columns are calculated from the average RMSD of all atoms of YA and the
indicated analogue (left axis). Light columns are calculated from only the backbone and QM regions of YA and the indicated
analogue (right axis). B) YA (red) and best analogue EVV (blue) superimposed (avg. RMSD 2.3 Å).
Assessment of Computationally Derived Geometries. The optimized structures of YA at the
B3LYP/d95(d,p):AMBER, B3LYP/6-311g(d,p):AMBER, and M06-2X/6-31+G(d):AMBER levels of
theory show a high degree of consistency and a low average RMSD (0.38 Å), suggesting a potentially
significant energy minimum (Figure 3A). It appears that YA can be divided into two sections. One section
is rigid with a helical structure and the other half resembles a flexible tail. In structured region, five well
defined hydrogen bonds are observed (1.88, 1.98, 1.91, 2.00, and 1.98 Å) and a single weaker hydrogen
bond (3.27 Å) links the flexible region to the structured region (Figure 3B). The volumetric isosurface
rendering of YA shows structural packing in the rigid region separate from the tail region (Figure 3C).
Figure 3. A) Blue, red, and green structures were calculated at the B3LYP/d95(d,p), B3LYP/6-311g(d,p), and M06-2X/6-
31+G(d) levels of theory with AMBER.B) Predicted hydrogen bonding. C) Volumetric density using isosurface mapping.

Conclusion
From among the original eight analogues, we identified two combinations that may serve as effective
mimics and retain its anti-cancer properties: [3]ΔEnv-[5]ΔVal-[10]ΔVal and [3]ΔVal-[5]ΔEnv,-[10]ΔVal.
Furthermore, the simulations predicted a structure of YA that was divided into two sections. One that was
more flexible and another region that was tightly held by intramolecular hydrogen bonding. Whether this
is characteristic of other low-energy conformations of YA will need to be explored in future studies as
well as its significance for bioactivity.
References
1. Shoemaker, R. H. The NCI60 Human Cell Line Anticancer Drug Screen. Nat. Rev. Cancer 2006, 6
(10), 813-823.
2. Kuranaga, T.; Sesoko, Y.; Sakata, K.; Maeda, N.; Hayata, A.; Inoue, M. Total Synthesis and Complete
Structural Assignment of Yaku’amide A. Journal of the American Chemical Society 2013, 135 (14),
5467-5474.
3. Dupredeau, F. Y.; Pigache, A.; Zaffran, T.; Savineau, C.; Lelong, R.; Grivel, N.; Lelong, D.; Rosanski,
W.; Cieplak, P. The R.E.D. Tools: Advances in RESP and ESP Charge Derivation and Force Field
Library Building. Phys. Chem. Chem. Phys. 2010, 12 (28), 7821-7839.
4. Cornell, W. D.; Cieplak, P.; Baylay, C. I.; Gould, I. R.; Merz, K. M. J.; Ferguson, D. M.; Spellmeyer,
D. C.; Fox, T.; Caldwell, J. W.; Kollman, P. A. A Second Generation Force Field for the Simulation
of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117 (19), 5179-5197.
5. Vreven, T.; Byun, K. S.; Komárnoi, I.; Dapprich, S.; Moontgomery, J. A. J.; Morokuma, K.; Frisch,
M. J. Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM. J.
Chem. Theory. Comput. 2006, 2 (3), 815-826.
6. Frisch, G. W. e. a. Gaussian 09, Revision B.01; Gaussian, Inc: Wallingford CT, 2016.
7. Khang, Y.; Byun, B. Assessment of Density Functionals with Long-range and/or Emperical Dispersion
Corrections for Conformational Energy Calculations of Peptides. J. Comput. Chem. 2010, 31 (16),
2915-2923.