Eliason, Joel
Weak Synchronization in Excitatory-Inhibitory Neuronal Networks
Faculty Mentor: Benjamin Webb, Mathematics
Introduction
One ubiquitously observed dynamic phenomenon in the nervous system is that of weak synchronization or clustering, a behavior in which a large group of neurons in a population will all fire synchronously and then fall out of synchronization. When isolated to neurons that only form short-range connections, this behavior is typically referred to as “neuronal avalanches”, and is thought to be particularly important for robustness of information transmission as well as sensitivity to inputs. Given these potential computational benefits, avalanches have been a focus of theoretical biologists for the past 20 years. In particular, my project focused on the conditions, parameterizations and network topologies (structures) under which neuronal avalanches arise. During the course of the project, I also gave attention to comparisons between different neuronal network simulation platforms, as well as investigating more deeply the relation between neuronal avalanches and “criticality”, a quality of dynamics that is often hypothesized to be the optimal regime for computation.
Methodology and Results
In this project, I relied on computer simulations of neuronal networks in several simulation languages, including NEST, Brian 2 and Nengo. Each of these languages is useful for simulating large heterogeneous networks of spiking neurons. Briefly, NEST is useful for speed and efficiency of simulation, as well as ease of network construction, Brian 2 is well suited to network visualization and customization of neuronal membrane dynamics and Nengo is designed to facilitate the construction of networks that are linear dynamical systems within the Neural Engineering Framework (NEF). These simulation languages allowed me to construct and simulate networks under different constraints and parameterization regimes.
Initially, I analyzed neuronal avalanches in very simple networks, such as randomly connected topologies and neurons that were connected in a ring. Typically, these neurons had very simple membrane dynamics and parameterizations, often modeled as linear ordinary differential equations. Such dynamical regimes often resulted in very simple homogeneous or predictable
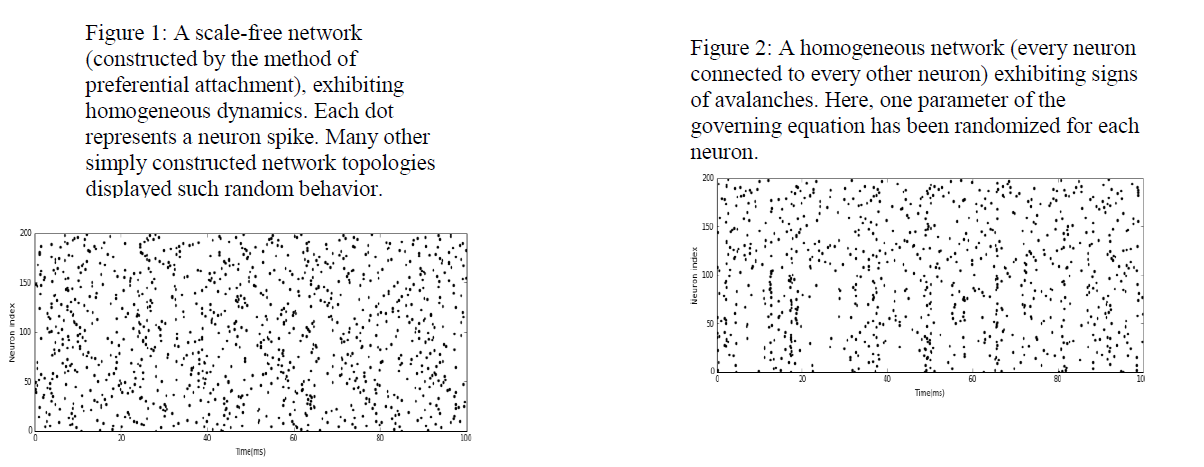
dynamics, as shown in Figure 1. Changing the equation that governed membrane dynamics in a randomly connected network offered the first signs of neuronal avalanches, as in Figure 2.
Indeed, in my simulations, such changes in population dynamics were usually most strongly influenced by changes in individual neuronal dynamics, rather than changes in network topologies (though some topologies did allow for more structured dynamics within a biologically realistic regime). Due to the “combinatorial explosion” that results from the very high-dimensional parameter space found in neural systems and my relative inexperience with such computational methods, I was not able to meet my goal of putting many constraints on topologies that would or would not exhibit avalanches.
Besides testing for neuronal avalanches within relatively simple topologies (all-to-all, random, preferentially attached and a simplified version of a visual cortex column), I investigated “self-organizing criticality”, in which networks evolve to more critical states over time. In particular, I tried to replicate the results by Xiumin and Small1, which claim that an all-to-all connected network of biologically realistic neurons connected with spike-timing dependent plastic (STDP) synapses will tend to a critical state (one in which neuronal avalanches are manifest according to a power-law distribution) when stimulated with a current of the appropriate amperage. However, after multiple attempts, I was unable to drive the network to a critical state. Similarly, after connecting the networks with static-weight synapses, changing the neuronal type or the connection scheme, I was also unable to find a critical state. Such negative results beg for further investigation, but they do lead naturally to the conclusion that the critical state, and the notion of “self-organizing criticality”, may be a more elusive phenomenon than is sometimes purported in the literature.
Beyond my tests in self-organizing criticality, I also examined the dynamics of linear systems designed in the NEF to perform certain computations or behaviors, such as integration or oscillation. Such circuits do exhibit much more complex behavior than the homogeneous dynamics observed so frequently; however, none of the computations that I examined showed signs of criticality or of operating in a critical computational regime. Since the NEF was not designed with advanced neural dynamics in mind, this makes sense; however, the fact that such behavior is not manifest can stand as a criticism of the NEF that, if addressed, would result in more biologically realistic circuits.
Discussion
The most striking conclusion that I came to in the course of this project was that neuronal avalanches were not nearly as ubiquitous as I had expected them to be. Part of this was the fact that the network topologies with which I was working were, for the most part, quite structurally simple. Furthermore, the equations governing connection and membrane dynamics live in a very large parameter space, and I may have simply been looking in the wrong places, parametrically speaking, for such critical behavior. However, in my last two experiments, I was able to show more conclusive results. The one that I am most excited about was the fact that “self-organizing criticality” seemed much more difficult to show than has been previously claimed. Since this is somewhat hotly debated within the computational neuroscience community, I look forward to extending this project in this direction and looking for further evidence for or against self-organizing criticality.
1Li, Xiumin, and Michael Small. “Neuronal Avalanches of a Self-organized Neural Network with Active-neuron-dominant Structure.” Chaos: An Interdisciplinary Journal of Nonlinear Science 22.2 (2012): 023104. Web.
