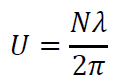Austin Maxwell and Julie Crockett, Department of Mechanical Engineering

Introduction

Internal waves are three dimensional waves that propagate within a stratified fluid. They are able to propagate in all directions within our atmosphere and the oceans which are both stratified fluids of continuously changing densities. Internal waves are much larger than surface waves, having wavelengths of hundreds of kilometers and amplitudes more than a kilometer in height. Due to their large size they can be difficult to study in nature, and there is still much to be learned about these waves and their impact on the environment. My research has focused on the generation of internal waves by the motion of large bodies (whales, submarines, etc.) within the ocean.

Methodology

The tests were performed in a long, narrow acrylic tank allowing the assumption to be made that the waves generated would only propagate in two directions. The waves were generated using an egg-shaped object as the large body model. The egg-shaped object measured eight centimeters in length and had a diameter of six centimeters. This was attached to a thin plastic filament that went through a three pulley system and was then attached to a weight. The pulley system allowed the egg shape to be pulled horizontally through the fluid by the free-hanging weight on the other end. A high speed camera (24 frames per second) was used to capture small displacements within the tank and motion of the model while tests were run.

The tank was filled based on the “revised ‘two-bucket’ method” discussed by Hill [1]. This allowed a constantly changing density of water to be added to the tank in order to model the density stratification found in the ocean.

After recording depth, densities, and model dimensions, I solved the following equation to find the maximum velocity that could be used at which internal waves would theoretically be generated.

N is the Brunt–Väisälä frequency at the model’s depth within the fluid which accounts for the density change. λ is the model length and approximate wavelength of our wave to be generated. By solving, I found that the model could not travel faster than 1.7 cm/s. I then determined a weight that would accelerate the model to that speed within the tank after 30 cm of travel.

To test, I first placed the model in the fluid to ensure it was neutrally buoyant. After letting the water in the tank settle for half an hour, I took pictures of the tank to be used as references in the image processing. The weight was then released and images were captured with the high speed camera to record the model motion, position, and water motion within the tank as the model was pulled across. This was repeated with breaks between tests for the water to settle. Then the tank water was mixed, and the tests were run again following the same process in the constant-density (Mixed) tank.

Results

Using image processing software called DigiFlow, I was able to analyze the motion within the body of water and showed that internal waves were formed. In order to determine the energy within the waves, I compared the difference of kinetic energy over a specified distance. Using the background image, I was able to compute the scale for each test set and calculate the velocity of the model at different points. Assuming that the turbulence, drag, friction, and other uncontrollable losses in the test were all the same in the mixed and stratified tanks, I assumed that the only difference in kinetic energy between the stratified and mixed tests should be due to the formation of internal waves in the stratified fluid. Based on this assumption, I found the change in kinetic energies over equivalent towing distances in the stratified and mixed tests.

Table 1: Week of 3-21-16 test results

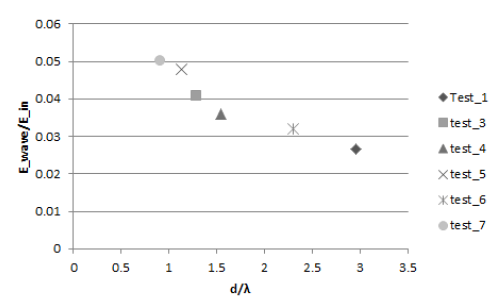
Figure 1 : Non-dimmensionalized results

 

Discussion

This series of tests has shown that large body motion within a stratified fluid does generate internal waves. Each test showed non-negative resultant wave-formation energy, meaning that some of the kinetic energy was lost in every test due to the formation of internal waves. As seen in the non-dimensional plot (Figure 1), there is a general trend that the energy ratio followed with respect to the distance towed. Table 1 shows there is a significant energy difference in stratified tests when compared with mixed tests. This energy goes into the formation of internal waves. When applied to large bodies, the energy could become significant in ocean environments.

Conclusion

Large body motion within a stratified fluid will generate internal waves. The energy in the internal waves increases with the distance of wave generation. Further testing should be done to validate these results, and to explore the effect of body size and input energy in the formation of internal waves.

Works Cited

[1] Hill, D. F. “General Density Gradients in General Domains: The “Two-Tank” Method Revisited.” Experiments in Fluids 32.4 (2002): 434-40. Print.