Jarrod Lund and Faculty Mentor: Oliver Johnson, Mechanical Engineering

Introduction

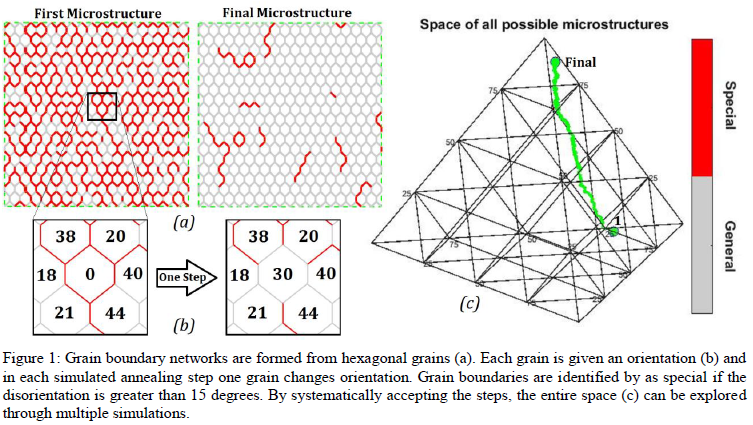
Within polycrystalline materials (e.g. metals and ceramics), grain boundary networks (GBN) influence the effective properties such as diffusion, conductivity, and crack and creep propagation¹. In precision applications such as jet engine turbine blades and solid oxide fuel cells, understanding and characterizing GBN are essential for better design. Modeling GBN allow for better exploration of the complex space of possible networks (figure 1d)². By modeling grains in a honeycomb lattice (figure 1a), grain boundaries can be identified by their misorientation angle (figure 1b). This can be a key indicator of the grain boundary’s properties. By combining information of the entire GBN, the effective properties can be determined.

Alternatively, by predicting the existence of a path of special or desirable grain boundaries via percolation, the same effective properties can be predicted much more quickly and easily. This is especially important when the effective properties vary by several orders of magnitude. Models have been proposed that include a percolation threshold (the percentage of special grain boundaries needed to percolate) in order to predict the effective property. However, this threshold is influenced by correlations within the network and is therefore unique for each network. In materials, crystallographic constraints and manufacturing process create correlations.

Methodology

We created a model that respects crystallographic constraints within the network by giving each hexagonal grain an orientation. We then created an annealing simulation that systematically accepts randomly assigned a single grain orientation to create all possible microstructures (figure 1). By creating a statistically significant number of microstructures, a percolation threshold can be found for different microstructures. We identified the microstructures by two variables. First, σ, which is defined by how segregated the special grain boundaries are from the general. Second, χ, which is defined by the shape of the clusters.

Results

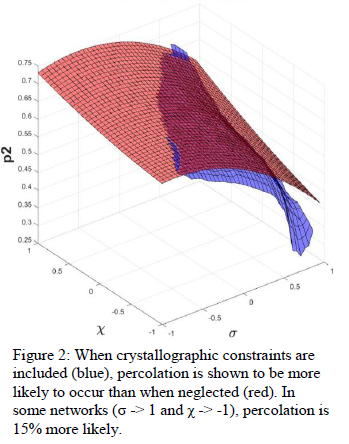
We compared our results that respected crystallographic constraints to a similar model that did not ³, and found that percolation is much more likely in crystallographically constrained microstructures than the idealized model for almost all types of microstructures (figure 2). We also found that the percolation threshold is not size dependent, although smaller microstructures are less constrained by crystallography. This results in improved accuracy using the percolation threshold as sample size increases. When 400,000 grains are used – which represents a 2 mm2 metal plate – the model is 98% accurate.

Discussion

We showed the importance of including crystallographic constraints when considering microscopic models of materials. Recent models have used correlations in an attempt to generalize material modeling. However, our result shows significant variation from this assumption and that GBNs must be considered as complex systems. Our model was designed for cubic microstructures with planar grains found in thin sheets of metals. However, the result shows the importance of crystallographic constraints within all GBN models. It also identifies topological areas where material design can occur (see figure 2).

Conclusion

As material design becomes more prominent with new manufacturing possibilities, understanding and modeling of GBN is essential for precision applications. By including crystallographic constraints in our model, we showed that percolation is more likely to occur, especially in certain areas of the design space. We thus highlighted an important factor in grain boundary engineering and an area for future exploration in design.

References

1. G. Gottstein, L.S. Shvindlerman, Grain Boundary Migration in Metals : Thermodynamics, Kinetics, Applications, 2nd ed., Taylor & Francis Group, 2010. http://swbplus.bsz-bw.de/bsz080396720cov.htm.
2. O.K. Johnson, L. Li, M.J. Demkowicz, C.A. Schuh, Inferring grain boundary structure–property relations from effective property measurements, J. Mater. Sci. 50 (2015) 6907–6919. doi:10.1007/s10853-015-9241-4.
3. M. Frary, C.A. Schuh, Percolation and statistical properties of low- and high-angle interface networks in polycrystalline ensembles, Phys. Rev. B. 69 (2004) 134115. doi:10.1103/PhysRevB.69.134115.