Andrew  White and Mark Transtrum, Department of Physics and Astronomy

Introduction

Observable biological behaviors result from the interactions of microscopic elements, which form complex systems that we can model mathematically. Ideally, mechanistic models should predict a biological system’s behavior without misrepresenting the system’s biochemistry. The method of model reduction known as the Manifold Boundary Approximation Method (MBAM) [2, 3] can help us identify which parts of a model are relevant for explaining a particular behavior. This project applies MBAM to gene transcription networks that exhibit a behavior known as “memory,” the ability to retain cellular decisions to activate or silence genes. We hypothesize that MBAM can help us model the behaviors of genetic “memory” systems in such a way that the resulting model accurately represents the systems’ underlying biochemistry. Furthermore, by applying MBAM to a hypothetical “Fully Connected Gene Network” (FCGN), we hope to reverse-engineer new gene network motifs that result in memory behavior.

Methodology

First, we construct mathematical models of three theoretical biological networks. In all three models, a deactivated gene X briefly activates long enough to switch the system to a permanent new state. The permanence of that switch is the desired memory behavior. The first two models are motifs known to display memory [1]. The first model (the “NF” model; see Fig. 1) features a double negative-feedback loop, in which genes Y and Z inhibit each other. This model, which initially starts in an “inactive-Y, active-Z” state, switches to an “active- Y, inactive-Z” state after X is activated. The second model (“PF”; see Fig. 2, left), on the other hand, features a double positive-feedback loop, in which Y and Z, after being activated by X, continue to stimulate each other. This model starts in an “inactive-Y, inactive-Z” state and ends with both permanently activated. We used Hill kinetics to model the production of the Y and Z gene products [1], with a degradation term to account for the rate of their intracellular degradation and dilution (see Fig. 1).

The third model is the FCGN model (Fig. 2, right). As the name suggests, the genes in this network are fully connected: each gene inhibits and activates all others. (Note that gene X is not inhibited or activated by other genes because it is assumed to be regulated upstream of the network.) Although 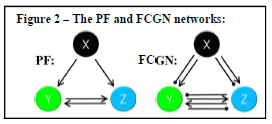biologically unrealistic, the FCGN contains most real three-node gene networks, and therefore should be reducible (via MBAM) to all three-node memory motifs.

After constructing mathematical models, we produce data for memory behavior, which we then use to find initial statistical fits for model parameters. Finally, if we can establish a model’s initial parameter values, we reduce the model by usinFg MBAM. While preserving a system’s memory behavior, MBAM guides model reduction by finding limiting approximations for the model’s parameters using computational techniques from information theory and computational differential geometry. (For a detailed discussion of MBAM’s implementation, see Asp 2016 [2].) The limiting approximations MBAM identifies allow us to remove and combine parameters, leaving only the connections relevant for characterizing each transcription network.

Results

Reduction of the NF model proved successful. In a series of MBAM-guided steps, we reduced the model from thirteen to seven parameters (Fig. 1). The new model can still fit the bi-stable “memory” data used for the original thirteen-parameter model. This is a major success because it is the first time MBAM has been used to reduce Hill kinetics models. For all three networks, fitting the initial model parameters to bi-stable data sets—i.e., the system stably remains in one state until gene X’s activation triggers it to switch to a second, equally stable (“remembered”) state—was unexpectedly difficult. We succeeded with the NF model, allowing us to proceed with MBAM reduction, but we failed to fit the PF and FCGN parameters to bi-stable data, preventing us from using them with MBAM techniques.

Discussion

The successful reduction of the NF network revealed that Hill kinetics can, in principle, be reduced using MBAM, evidencing MBAM’s usefulness to biological modeling. However, our inability to fit the PF and FCGN models to bi-stable data may reveal something deeper. Previous applications of MBAM to systems biology have only involved Michaelis-Menten kinetics models [2], which are exponentially simpler than Hill kinetics models. Additionally, the data sets in this experiment are bi-stable, and initial parameter estimation was harder than in previous MBAM applications where initial parameter values could even be chosen randomly [2]. Taken together, these unique factors may indicate that fitting Hill kinetics to bi-stable data requires a fundamentally different approach than other MBAM applications.

Conclusion

Although we did not discover the new genetic memory motifs we hoped for, this project’s success in reducing the NF model does indicate that MBAM can be used reverse-engineer gene memory networks and other Hill kinetics models. Additionally, the research reveals the difficulty of fitting Hill kinetics to bi-stable data, as seen in the cases of the PF and FCGN models. The selling point of the MBAM method is that it can guide model construction without the modeler knowing a system’s biochemistry a priori. However, there is clearly a need for a better theoretical approach to picking initial parameter values for data fitting. This research has opened the door for a more theoretically rich understanding of the obstacles to using MBAM to reverseengineer network motifs for complex behaviors, such as genetic memory.

References

1. Alon, U. (2006). An introduction to systems biology: design principles of biological circuits. CRC press.
2. Asp, Merrill. “Adaptation in Enzyme Networks: Searching for Minimal Mechanisms.” Thesis. 2016. <https://www.physics.byu.edu/faculty/transtrum/pubPDF/MAsp2016.pdf>.
3. Machta, B. B., Chachra, R., Transtrum, M. K., & Sethna, J. P. (2013). Parameter space compression underlies emergent theories and predictive models. Science, 342(6158), 604-607.