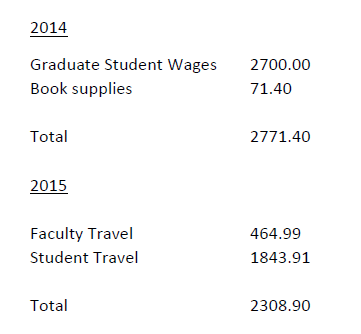Faculty Advisor: Denise Halverson
1. Evaluation of how well the academic objectives of the proposal were met
The goals for the mentoring environment were reached:
- Academic Development – Each student had the opportunity to work on a cutting edge research problem, as indicated below. Papers are in various stages of completion, a few submitted or accepted for publication, but all have drafted papers.
- Community Development – Several students were able to attend the MAA Math Fest in both 2014 and 2015. Most students gave presentations at the CPMS Student Research Conference. My students have been able to interact with engineering student working on similar projects. We have also had several consultation session with Robert Lang, a renowned origami mathematician.
- Spiritual Development– A key component of this mentoring environment was the teaching/learning/practicing of leadership skills. I took the opportunity at least once a week to teach a personal or professional leadership skill which the students could incorporate in their lives. We studied Steven Covey’s “Seven Habits of Highly Effective People” and Liz Wiseman’s “Multipliers” along with other concepts supporting the Mission and Aims of Brigham Young University. Our trips to the national MAA Math Fest conference gave the students opportunities to be ambassadors of BYU and the gospel of Jesus Christ. The students did an exceptional job not only in mathematics, but in their example in the way were reaching out to others and conducting their lives.
2. Evaluation of the mentoring environment
A positive, engaging experience was provided for students and the students were very enthusiastic about their research.
Our goal was to give the students the opportunity for each week to have: (1) at least 1 hour of small project group time with me in order to ask questions, discuss ideas, assess progress, etc.; (2) a 1 hour seminar meetings with the entire research group to learn and share ideas with other participants; and (3) at least 3 hours of work sessions time with the other students in their group to work together on the research problems. The remaining hours per week will be individual time for each student to work on his/her own particular aspect of the research problem. We stayed fairly close to this goal, only offsetting according to student needs.
During the weekly group meetings, students gave presentations and reported on their progress. This provided the students with the opportunity to effectively communicate their ideas and learn from others. During these meetings, students were actively involved in asking their own questions and in brainstorming on how to attack unsolved problems. As the students made significant advances on their problems, they wrote up their results to submit for publication. They also participated in conferences sponsored by the CPMS college and the mathematical community.
Finally, I have been enthusiastically supportive of the idea of incorporating spiritual learning in an academic setting and that this is fundamental at BYU. We invite the influence of the Spirit by beginning our large group meetings with prayer. We strive to apply gospel principles in all aspects of our lives. My students have been excellent ambassadors of the Church, as we have interacted with others in the greater community. I also incorporated training on leadership skills, supported by gospel principles, that will help them be resilient in leading out by their example in the way they live their own lives. I have received very positive feedback, including unsolicited notes of appreciation from the students, for this aspect of their training
3. List of students who participated and what academic deliverables they have produced or it is anticipated they will produce
List of Students and Projects
Graduate
- Alex Saftsten, 2015 Summer Research Group TA
- Andrew Logan, 2014 Summer Research Group TA
Undergraduate
- Reese Berry and Eric Moss, Muira-Ori and Mars origami patterns
- Shawn Green, Courtney Hoagland, Huffman grids
- Paul Gibby, Brent Mabey, The buckling of the twisting cubetower
- Jennifer Bickham and Amber Chase, Thick origami folding
- Alex Safsten and Logan Tathum, Variational and Numerical Approaches to the Extreme Deflection Problem.
- Alex Safsten, Travis Fillmore, and Andrew Logan, Analytical Modeling of Energy Minimums in Kaleidocycles
- Robert Jordan Porter, and Austin Unsicker, Rigidly Reachable Folding Patterns in Origami
- Alex Safsten, Logan Tathum, and Andrew Logan, Thick origami
- Jennifer Bickham and Travis Fillmore, The n-Jointed Kaleidocycles for n>6.
- Andrew Logan, The three-point Steiner Problem on a flat torus
Presentations
Student presentations:
- Jordan Porter, Origami Mathematical Applications and Rigid Reachability, MAA Math Fest, August 2015. (MAA Outstanding Presentation Award)
- Alex Safsten, Techniques for Solving Generalized Elastica Problems, MAA Math Fest, August 2015.
- Logan Tatham, A Topological Approach to the Existence of Solutions of Calculus of Variations Problems, MAA Math Fest, August 2015. (MAA Outstanding Presentation Award)
- Jennifer Bickham, Problems with the Rigid Foldability in the Symmetric Thick Bird Foot Folding Pattern, CPMS Student Research Conference, March, 2015.
- Andrew Logan, The Steiner Problem on Closed Surfaces of Constant Curvature, CPMS Student Research Conference, March, 2015. (Session Winner)
- Jordan Porter, Applied Origami and Rigid Reachability, CPMS Student Research Conference, March, 2015. (Session Undergraduate Winner)
- Alex Safsten, Solutions to Nonlinear Extreme Deflection Problems, CPMS Student Research Conference, March, 2015.
- Amber Summers, Nonsymmetric Thick Folding Dilemmas, CPMS Student Research Conference, March, 2015.
- Logan Tatham, A Topological Approach to the Existence of Solutions of Calculus of Variations Problems, CPMS Student Research Conference, March 2015.
- Jennifer Bickham, Matrix Method Kinematics and the Bennett Linkage, CPMS Student Research Conference, March 2014.
- Andrew Logan, The Three Point Steiner Problem on Surfaces with Constant Curvature, CPMS Student Research Conference, March 2014.
- Jordan Porter, Solar Arrays and Rigid Rechability, CPMS Student Research Conference, March 2014.
- Travis Fillmore, Modeling Energy Minimums in Bennet Linkages, CPMS Student Research Conference, March 2014.
- Alex Safstem, Analytically Modelling Energy Minimums in Kaleidocycles, CPMS Student Research Conference, March 2014.
- Logan Tatham, Solutions to Extreme Deflection Problems, CPMS Student Research Conference, March 2014.
- Austin Unsicker, Applied Origami and Injectivity, CPMS Student Research Conference, March 2014. (Session Undergraduate Winner)
Papers Published or Accepted for Publication:
C. Safsten, T. Fillmore, A. Logan, D. Halverson, L. Howell, Analyzing the stability properties of kaleidocycles, accepted to the Journal of Applied Mechanics, January 2016.
C. Alex Safsten, Logan C. Tatham, A variational approach to a generalized elastica problem, accepted for publication in Involve June 2015. (Advisor: Denise M. Halverson)
Papers Submitted:
D. M. Halverson, A. E. Logan, The three-point Steiner Problem on a flat torus, submitted for publication to Involve, April 21, 2015.
Papers in Progress:
Reese Berry, Eric Moss, Denise M. Halverson, Generalizing Muira-Ori and Mars origami patterns, in progress.
Shawn Green, Courtney Hoagland, Denise Halverson, Generalization of cylindrical Huffman grids, in progress.
Paul Gibby, Brent Mabey, Denise M. Halverson, The buckling of the twisting cubetower, in progress.
J. Bickham, A. Summers, D. Halverson, Thick folding dilemmas, in progress.
D. M. Halverson, T. W. Hills, R. J. Porter, A. A. Unsicker, Rigidly reachable folding patterns in Origami, in progress.
4. Description of the results/findings of the project
Kaliedocycle Project – Kaleidocycles are continuously rotating n-jointed linkages. We considered a certain class of 6-jointed kaleidocycles which have a spring at each joint. For this class of kaleidocycles, stored energy varies throughout the rotation process in a non-constant, cyclic pattern. We provided a model and an analysis of the stored energy of a kaleidocycle throughout its motion. In particular, we solved analytically for the number of stable equilibrium states for any kaleidocycle in this class.
Rigid Reachability Project – We developed a method for detecting rigid reachability of folding patterns. We applied this method to a single vertex 4-valent pattern and a pseudo-square twist, a 4-vertex 4-valent pattern. This method generalizes to any folding pattern with a single degree of freedom, and can adapt to folding patterns of multiple degrees of freedom.
We also demonstrated that certain solar array pattern were not rigid reachable from a geometric analysis.
Extreme Deflection Project – We employed calculus of variations to find the shapes to which material conforms under an extreme deflection. We derived a system of nonlinear differential equations which, after setting boundary conditions, will plot the deformed material in the xy – plane. We also presented a general solutions to these equations. Finally, we examined numerical methods for approximating solutions to fit these equations to boundary conditions.
Thick Folding Projects – We proposed several strategies and built models for thick patterns generalized from rigid reachable flat patterns. We demonstrated that the thick folding for the bird foot pattern is not rigid reachable. We utilized both geometric and analytic methods.
Folding Patterns Arising from Tesselations – We investigated the possible construction for Muira-Ori and Mars origami patterns and Huffman grids. We also analyzed the buckling of the twisted cube tower.
5. Description of how the budget was spent
Please note that I have not yet spent funds from my MEG grant on undergraduate student wages for the mentoring environment that I set up as a result of receiving this funding. My department chair requested that department funds for student mentoring be spent in lieu of this grant money. Thus I still have funds to continue this project with upcoming students.
Also, summer programs were funded by an NSF EFRI-ODISSEI grant.