Adam Kingsley and Faculty Mentor: Dallin Durfee, Physics and Astronomy
I. Introduction
In 1956, Hanbury Brown and Twiss (HBT) published a paper1 on a method of determining the angular size of a star by comparing the intensities gathered from two detectors. They used this effect by using two photomultiplier tubes and by increasing the distance between them, saw a drop in the correlation between the currents. Because the correlations are made by the interference at the detectors but only the intensity is measured, the effect is sometimes referred to as intensity interferometry.
The idea arose to use the HBT effect to teach undergraduates various principles of light in a lab setting. The application of this effect would allow students to experiment easily with temporal and spatial coherence, correlation, angular size and the frequency spectrum of light.
II. Methods
We have made a thorough analysis of this project and determined that it is feasible. Here we give a mathematical overview of the correlation function then a description of the method by which we will imitate a chaotic light source with a laser. The mathematical principle used by the HBT effect is the relation between the first- and second-order correlation functions for chaotic light. The first-order correlation function2 is described as
where E1(t) and E2(t + τ) denote the electric field at detector 1 and 2 separated by a time τ, and < > represent time averaging the signal over many coherence times of the light. The second-order correlation function is written similarly but with the electric fields replaced with intensities. I have discovered that the relation2 governing the signal-to-noise ratio will be:
where tc is the coherence time of the light and Tr is the time response of the detector. Thermal light has a coherence time on the order of a femtosecond and the faster detectors in our lab have a time response of 20 ns making tc/Tr approximately equal to 5 x 10-8. To see the signal would require very long integration times which is not optimal for an instructional lab. The solution is to instead lengthen the coherence time.
A laser would have a long coherence time but the light would be spatially correlated across the aperture and the correlation would never drop off despite separating the detectors. The solution is to spatially modulate the laser beam so that the light is uncorrelated across the aperture.
I have conducted a numerical analysis of several situations to determine a reasonable bandwidth of frequencies that would allow us to easy detect the correlation. Through these calculations I have found that I need a bandwidth that is smaller than the bandwidth of my detectors. For this reason we are going to use a laser and by sending the beam through a spinning disk we can control the spatial fluctuations and thus effectively control the bandwidth. To understand this method the laser can be seen as a carrier wave that we have introduced fluctuations onto.
III. Results
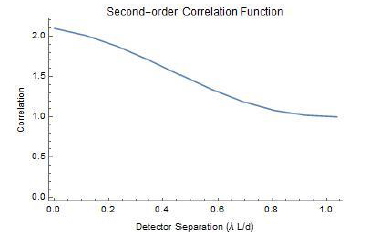
I modeled this numerically by creating a randomized wave with a bandwidth of 200 kHz. I split the source into 100 equal portions and generated a wave for each portion. I then by calculating relative distances between the sources and several other points, generated the intensity patterns at 30 points along a range. I used the above mentioned equation to calculate the correlation of the intensities. The resulting graph of the correlation is shown below. For convenience the x-axis is shown in units of the linear Rayleigh criterion.
IV. Conclusion
We have acquired analog multiplier chips that have a bandwidth much greater than the time scale of fluctuations we plan to introduce onto the coherent source. We attempted to procure a portable laser that had sufficient power output so that the small amount that came out the aperture would still be sufficient, but the laser we purchased did not perform to specifications.
We have considered the idea of using the line-in port on a computer to gather the data so that the correlation can be digitally calculated. This would make the experiment much easier to assemble since the students’ equipment would consist of just the photodiode and the computer. A high-powered laser pointer still needs to be acquired and the light source assembled. The apparatus may be complex in assembly but if successful it will simplify the data acquisition. The project must now be continued by another student.
1 Hanbury Brown, R., and R. Q. Twiss. “A Test of a New Type of Stellar Interferometer on Sirius.” Nature 178.4541 (1956): 1046-048. Web.
2 Rosenblum, Serge. “Lecture 6: Bunching, Antibunching and the HOM Effect.” (n.d.): n. pag. 2012. Web. 14 Aug. 2015.