David Squires and Faculty Mentor: Justin Peatross, Department of Physics and Astronomy

Introduction

In this mentored research project, we investigated how intense laser light is scattered by samples of gas. In particular, we measured light scattered in non-phase-matched directions perpendicular to the laser beam.

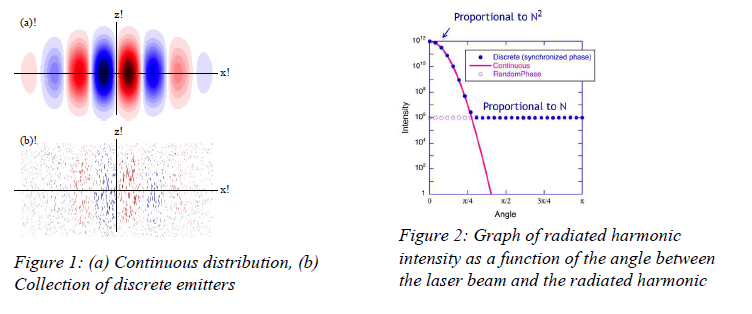
According to classical phase matching, the intensity of light scattered from a sample depends on whether the sample is best approximated as a continuous medium or a collection of discrete emitters (Figure 1). In the former case, as the angle between the phase-matching direction and the radiated harmonic approaches π/2 radians, the intensity of that radiated harmonic light approaches 0. In the latter case, the light intensity reaches a minimum value near π/2 and remains at that intensity. In addition, the intensity of the radiated harmonic from the array of discrete emitters (such as gas molecules), should vary linearly with the number of atoms stimulated by the laser (Figure 2).

Methodology

In order to test the prediction for gas molecules, which we modeled as discrete emitters, we measured 3rd harmonic photons out the side of a laser focus in a chamber filled with high-purity helium (Figure 3). The photons were collected by an aspheric lens and imaged through a slit parallel to the laser beam. The collected photons were then collimated and sent through a transmission grating. Finally, the light was focused to a photo multiplier tube (Figure 4). We then measured the third harmonic signal as a function of pressure. The number of atoms in the laser focus can be easily derived from the pressure of the gas in the helium chamber.

Results

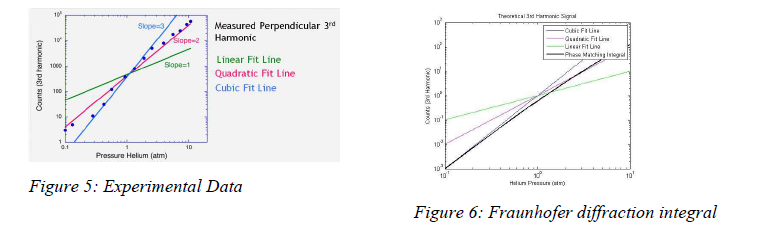
Data from our photo multiplier tube indicate that the radiated harmonic signal varies neither linearly nor quadratically with pressure (Figure 5). Instead, the data appear more quadratic at low pressures and more cubic at high pressures. This surprising result can be explained by considering that the intensity of the laser generating the measured 3rd harmonic varies along the dimensions of the laser focus. A fraunhofer diffraction integral taking this variable intensity into account generates a predicted signal that agrees with our experiment (Figure 6).

Discussion

While the project succeeded in producing a theoretical model for harmonic emission that agrees with experiment, we still need to quantify the accuracy and precision of the model as well as gather more data points from a larger range of pressures in order to confirm the usefulness of our model. In addition, we have yet to confirm that the model applies to radiated harmonic light from other gas samples, such as argon, air, etc.

Conclusion

As circumstances changed in the lab, the goals and methods of this project changed a great deal from the originally proposed project. However, we succeeded in developing a model that can be used to predict harmonic light emission as a function of the number of emitters in a laser field.