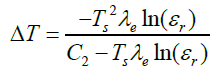Joshua Schmidt and Matthew Jones, Mechanical Engineering

Introduction

Pyrometers are an instrument used to infer the temperature of a surface without direct contact. Typical pyrometers use a single infrared color band to measure the radiation emitted from the surface, thus inferring the surface temperature. Two color pyrometers utilize two separate infrared color bands which can increase accuracy and are especially useful when the emissivity, or a surface’s ability to emit radiation, is unknown. However, the value of the inferred temperature is only useful if there is a valid model governing the temperature measurement. To determine validity, sources of error must be identified and explored. For this project, a mathematical model was developed for the apparent temperature from a two color pyrometer, and the sources of error in temperature readings were analyzed. Finally, an equation to determine approximate error in any given temperature reading from a two color pyrometer was developed.

Methodology

A model was made using the definition of irradiation to solve for surface temperature, resulting in the temperature error shown in the equation below.

During analysis, there were several assumptions made. The first assumption was that the irradiation incident on the detector is only due to the emission by the surface. As others have explored the validity of this assumption, it was not explored in this project. It was also assumed that the solid angle intended by the detector was very small. This assumption was also not discussed in this project. An assumption used to simplify the model was Wein’s approximation that . The effect that this assumption has on the resulting temperature reading was explored by xamining the difference between Wein’s approximated irradiation ratio and the actual irradiation ratio and then exploring its effect on temperature reading. This was done for a set of variables commonly seen in two color pyrometers.

As can be seen in the error equation previously shown above, the error is a function of surface temperature, effective wavelength, and emissivity ratio. The effect of these variables were discovered by holding two constant at a time and finding the effect of the apparent temperature over a range of the variable being explored. With this information it could be determined which variable most affected the apparent temperature reading.

Results

Wein’s approximation was found to be less valid as surface temperature increased. This was to be expected as the power of the exponent is inversely proportional to surface temperature. Thus as surface temperature increased, the difference between the Wein’s approximated irradiation ratio and the actual irradiation ratio increased. It was shown that even with an emissivity equal to one, the apparent surface temperature could be off by very significant amounts. The author found some readings to be off by more than 160 K. However, when compensated by using small wavelengths for measurement, the error becomes insignificant.

The most significant source of error was when the emissivity ratio was not equal to one. Very small changes in emissivity ratio drastically increased the temperature error as shown in the figure below.

Figure 1: Temperature error in relation to emissivity ratio. As can be seen by the figure, error becomes very significant with slight changes in ratio. The chart assumes λ=0.9 μm, Δλ=0.2 μm, and Ts=1000 K.

Error was also found to increase with increasing surface temperature. It was also found that error increases with increasing wavelength measurement, but decreases with increasing wavelength spread. Thus choosing a small initial wavelength and a large step in wavelength produced the most accuracy.

Finally, an estimation of error equation was found as shown below.

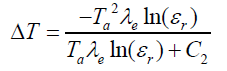
The equation assumes knowledge of apparent temperature and wavelengths and requires a guess of emissivity ratio.

Discussion

The results of this project show that the most accurate temperature readings can be done at low temperatures and at low wavelengths with a large Δλ. As it is more desirable to use pyrometry at high temperatures, this cannot always be achieved. Thus it is important to have an understanding of the spectral irradiation curve and chose wavelengths that will produce the greatest ratio of irradiation. It is also desirable to have knowledge of the spectral emissivity curve when choosing measurement wavelengths.

Conclusion

With a valid model and knowledge of error sources, two color pyrometry will be more useful when taking temperature measurements.