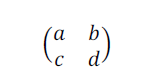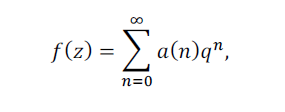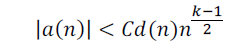Kyle Pratt and Dr. Paul Jenkins, Department of Mathematics
Modular forms are complex analytic functions with remarkable properties. Modular forms possess interesting and surprising connections to many different branches of mathematics. For example, it is well-known that Andrew Wiles’ proof of Fermat’s Last Theorem, a conjecture that had been unresolved for more than three centuries, utilized modular forms in a crucial way.
A modular form is a holomorphic function f(z) on the complex upper half-plane that satisfies the transformation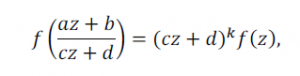
for a positive integer k. Here the matrix
is contained in some subgroup G of the group of matrices with integer entries and determinant 1. As a result of this functional equation, a modular form can be written as a Fourier series. We write
where
and n0 is some integer. We call the a(n) the coefficients of f(z). Often the coefficients of a modular form carry interesting arithmetic information, and it is natural to ask how large the coefficients of a modular form can be.
The modular form f(z) is a cusp form if it vanishes at the cusps of G (this is a technical notion which we leave undefined for simplicity). Cusp forms are extremely important in the study of modular forms, and their coefficients have been widely studied. Deligne [De] showed that for any cusp form of weight k we have
where C is a constant depending f(z), and d(n) is a certain arithmetic function. In [JR] the authors studied the size of C for f(z) a cusp form of the full modular group and arbitrary k. For my project I studied the constant C for modular forms of “level 2” (for simplicity we also leave this term undefined). In particular, I proved the following theorem.
Let k ≥ 8 be an even integer, and let G be a cusp form of weight k and level 2. If we write
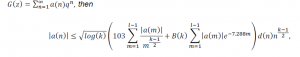
where B(k) is an explicitly given function and l is an explicit integer given in terms of K.
The proof of the theorem mainly uses the ideas of [JR], but there are several complications that arise from the fact that we are dealing with level 2 modular forms. In dealing with these issues I had to prove new lemmas about the zeros of certain