John Gardiner and Jean-Francois Van Huele, Physics and Astronomy

Introduction
Entanglement is a quantum phenomenon that is important to many applications including quantum computing and cryptography. The way that a quantum system changes in time is encoded in a mathematical object called the Hamiltonian of the system. The goal of this project was to better understand the relation between the quantum dynamics of a system, as described by the Hamiltonian, and the entanglements that arise in the system, with the bigger goal of better understanding how entanglement changes in time. To this end I studied computer simulations of simple quantum systems to observe how certain features of the Hamiltonian were reflected in the ensuing entanglements.

Methodology
Using the MATLAB language I wrote a script that simulates a quantum system of three qubits. The program takes as input an initial state for the three qubits as well as a Hamiltonian specifying the dynamics and then calculates the changing state as time progresses. A three qubit system is the smallest quantum system that contains more than two disjoint subsystems.

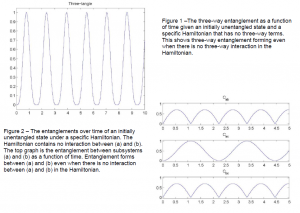
I wrote scripts to calculate the different entanglements present in the system. Between the three qubits there are four entanglements. If we label the three qubits (a), (b), and (c) then the entanglements are the two-way entanglements between (a) and (b), between (b) and (c) and between (a) and (c), as well as a three-way entanglement between (a), (b) and (c). There are many ways in which entanglement can be quantified. We chose a measure of entanglement called concurrence for the two-way entanglements and a measure called three-tangle for the three-way entanglement.

Results
With the simulation we were able to ask and answer some simple questions. For instance, “Can three-way entanglement arise from an initially unentangled state evolving under a Hamiltonian with no three-way interaction?” We found that Hamiltonians containing only two-way interactions can indeed generate three-way entanglement (See Figure 1). Another question was whether entanglement can be generated between two subsystems when the Hamiltonian does not contain a direct interaction between the two subsystems. We found that it such an entanglement can arise (See Figure 2). I was able to present the proposed simulation and the above mentioned results at the APS Four Corners regional meeting in Denver, Colorado and the BYU Student Research Conference.

Discussion
The example results mentioned above show that there is not a one-to-one correspondence between the interactions in the Hamiltonian and the entanglements that arise; specific entanglements can arise between subsystems even when the corresponding interaction terms are absent from the Hamiltonian. This suggests that the relation between the quantum dynamics and the entanglement in a system are not as simple as might be naively supposed. This simulation will continue to serve a purpose. There are further questions that my mentor and I hope to answer with this simulation. Though some simple and specific questions were answered, we have not answered the broader questions. One such question the extent to which the interaction in the Hamiltonian can be specified given the entanglements over time.

Conclusion
My mentor and I were able to ask and answer specific questions about the relationship between quantum dynamics and entanglement via a simulation of a simple quantum system.