Braden Hancock and Dr. Christopher A. Mattson, Mechanical Engineering Department
Introduction
Nearly one year ago, we proposed the development of a mechanism for evolutionary optimization that would provide the widely recognized benefits of ε-dominance methods while simultaneously supporting Pareto knee exploitation. Thanks to the ORCA grant that we received to pursue this research opportunity, we were able to develop that technology and disseminate it in the scientific community. The results of this research include a peer-reviewed journal article, a professional conference paper, two “Best Paper” awards at regional student conferences, an invitation to compete in an international student conference in Jan. 2015, and an Honors thesis.
Methodology
In Evolutionary Multi-Objective Optimization (EMO), the ε-dominance mechanism has been heavily researched and frequently used as a means of promoting diversity among solutions and a guarantee of convergence at a reasonable computational cost. The fundamental concept of this mechanism is that the design space is divided up into a grid of contiguous boxes of side length ε, and no more than one Pareto solution is permitted per ε-box. When this restriction is enforced within an evolutionary optimization algorithm, the result is an approximately equally spaced distribution of solutions along the Pareto frontier. However, multiple studies have shown that designers tend to select solutions that are located on “Pareto knees,” regions of the Pareto frontier that “bulge” out toward the utopia point.
In our research, we investigated the effects of replacing the ε-box with a new shape that would naturally promote a higher concentration of solutions in these desirable regions. We found that the convergence and diversity benefits of ε-dominance could be maintained while simultaneously allowing for exploitation of (i.e., a higher concentration of solutions in) the Pareto knees regions. The shape we discovered is called a Lamé curve (shown in Fig. 1). Like the ε-box, it is easily defined by user parameters to reflect the scaling of the objectives that define the design space. When centered on a Pareto solution and applied as a restriction, the Lamé curve naturally leads to more space between solutions in flat regions of the Pareto frontier, and less space between solutions in the knee regions.
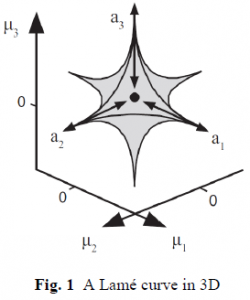
Results
To confirm our hypothesis about the performance of L-dominance (essentially ε-dominance but with Lamé curves in place of ε-boxes), we performed simulations with each mechanism on 5 test problems from the literature. For each problem, we arbitrarily selected a target resolution for the knee region, then calculated the necessary parameters to achieve that resolution using both L-dominance and ε-dominance. Shown below in Table 1 are the number of function calls required by each method to reach convergence. Because ε-dominance yields only uniform distributions, it necessarily had to generate more solutions overall in order to achieve the same knee resolution as L-dominance. Importantly, as dimensionality increases, so does the relative reduction in function calls provided by L-dominance.
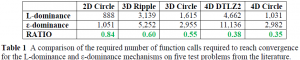
Conclusion
Based on our findings both analytically and computationally, we confidently recommend the use of L-dominance as a replacement for the widely used ε-dominance mechanism in EMO methods, particularly for problems with high dimensionality.
Broader Impact
Soon after submitting my ORCA grant application, I was approached by Tim Nysetvold, a freshman mechanical engineering student who was interested in our research. I invited him to work alongside me on this project and enjoyed the opportunity to be a mentor myself, preparing him to be the lead presenter at one of the student paper competitions where we won the 1st Place Best Paper award.
Publications and Awards
The results from this research have been published/presented in the following venues or have been submitted/accepted (as indicated) for future publication:
- Hancock, B. J., T. B. Nysetvold, Mattson, C. A., “L-Dominance: An Approximate-Domination Mechanism for Adaptive Resolution of Pareto Frontiers,” 15th AIAA Multidisciplinary Analysis and Optimization Conference, Jun. 2014 (MAO-1890284)
- T. B. Nysetvold, Hancock, B. J., Mattson, C. A., “A Novel Evolutionary Optimization Mechanism with Pareto Knee Exploitation,” ASME Old Guard Oral Presentation Competition 2014—Utah Section
- Hancock, B. J., T. B. Nysetvold, Mattson, C. A., “An Approximate Domination Mechanism with Pareto Knee Exploitation,” AIAA Region VI 2014 Student Conference
- Hancock, B. J., T. B. Nysetvold, Mattson, C. A., “L-Dominance: An Approximate-Domination Mechanism for Adaptive Resolution of Pareto Frontiers,” Structural and Multidisciplinary Optimization, (Revisions Submitted Oct. 2014)
- Hancock, B. J., T. B. Nysetvold, Mattson, C. A., “An Approximate Domination Mechanism with Pareto Knee Exploitation,” AIAA International Student Conference 2015, Jan. 2015 (By invitation for winners of regional conferences)
- Hancock, B. J. “Obtaining Smart Distributions of Pareto Solutions in Multiobjective Optimization through the use of Lamé Curves,” Brigham Young University, Department of Mechanical Engineering, Undergraduate Honors Thesis, (Scheduled for Jan. 2015)
