Jazz Myres and Dr. Kent Gee, Department of Physics and Astronomy

Introduction

According to the Office of Naval Research (ONR), the United States Department of Veteran Affairs spent over $1 billion dollars on military hearing loss compensation in 2010 alone1. A major cause of hearing loss is exposure to high Sound Pressure Levels, which are caused by military aircraft. These severe levels and high risks are what motivate the overarching goal of all jet noise research: to attenuate the sound impact and reduce the risk of hearing loss. My research project helps this overall purpose by characterizing jet noise and innovating more complete methods of jet noise study. The purpose of this project is to temporally correlate and analyze a large set of military jet noise data for the Office of Naval Research.

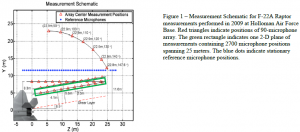
The specific problem my project addresses is temporally correlation of large-scale scanbased acoustic measurements. When data is taken in groups at different times, there is intrinsic difficulty in aligning those measurement signals in time. This alignment is necessary for phasedependent measurements such as acoustical holography, partial field decomposition, and wave propagation studies; and is typically performed using reference microphones. Figure 1 illustrates a large-scale measurement of an F-22A Raptor. For extended, turbulent sources many reference microphones are needed; in this case the estimated cost of the reference microphones is $500,000 to the test. For this project, I developed a novel method of using self-referencing for spatially related scans that eliminates the need for costly reference channels in phase-dependent analysis.

Methodology

To self-reference measurement scans, the aforementioned F-22A raptor data was used. The fully temporally and spatially correlated array was achieved through a 4-step process. The first step is to unwrap the phase of individual scans in a single position (in this case, each scan contained 90 microphones). The second step is to stitch together the amplitude of all scans in the array. The third step is to stitch together the phase of all scans in the array. All of these steps are performed on a complex pressure for one frequency block and one time bin of the frequencydomain data. The final step is to ensemble average the stitching results to obtain a complex pressure that represents the entire waveform.

First, the phase of each scan must be two dimensionally unwrapped. This is a formidable problem in signal processing because following a continuous unwrapping path leads to propagated erroneous discontinuities in phase that can be caused by signal noise, abrupt changes in signal, or under sampling. These problems were resolved using a robust 2D unwrapping algorithm developed by the Liverpool John Moores University Coherent and Electro-Optics Research Group for optical unwrapping problems2. This algorithm uses a non-continuous unwrapping path, beginning with the regions of greatest phase discontinuity. It is robust and operates at high speed, accurately unwrapping the phase of a two dimensional measurement array. The next step is to stitch the amplitudes of adjacent scans. The F-22 test was designed such that adjacent scans had regions of spatial overlap. The energy average in these regions of overlap was matched, adjusting each scan so that the areas of overlap matched energy. The total energy across the aperture was unchanged, maintaining the integrity of the measurements. This method allows for the directivity of the signal to stay intact.

Finally, phases of adjacent scans are stitched together using the algorithm I developed over the course of this project. This stitching method eliminates the need for costly reference channels and can be used for many types of scan-based measurements. The algorithm is used by finding mean differences between overlapping regions of adjacent scans and applying these phase differences to adjust scans. This shift is propagated through all scans in the array. Beginning in the region of the array with the least signal noise is optimal to avoid propagating noise throughout the array. Each scan in the two dimensional array is affected by the three scans adjacent to it in the direction of propagation. Using all of this data ensures complete phase information is included in each measurement.

The result of these methods is a spatially large two-dimensional array of data, that would be impossible to acquire at one time, that represents the sound filed on the plane as if it were taken in a single measurement. The efficacy of these results has been tested in the performance of phase-dependent analysis such as acoustical holography. It is also being tested in a laboratory test in BYU’s anechoic chamber facilities. See figure 2. These test results are forthcoming.

Results

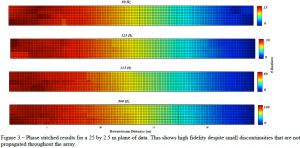
Results of the stitched phases for different frequencies are shown in figure 3. The phase shown is smooth across all 30 scans contained in the plane. There are some discontinuities in phase between scans, but they are minor and do not propagate. These are smoothed out as the phases for all blocks are ensemble averaged. The impact of these results also affects the accuracy of acoustical holography. One of the requirements of acoustical holography is that the energy in the target region must all be contained within the reference region. When a 1D reference array is used to reference a 2D target array, this condition is not met. If the 2D array is used as a selfreference, there is a guarantee that all of the energy is represented in the reference. I presented these results at the Acoustical Society of America’s international conference. It is anticipated that a JASA article will be published in 2014. I will also be able to present this upcoming semester at the Utah Conference for Undergraduate Research regular session and women’s conference as well as the Student Research Conference at BYU.

Conclusion

This algorithm succeeds for frequencies low enough that there are no ground reflection interference nulls, there exists good spatial resolution in the microphone spacing such that there is a minimum of two microphones per wavelength, and that there is good local coherence in the signal. Fortunately this is also the requirement for phase-based analysis.

The benefit of using this method of self-referencing is to avoid the cost, time, and complication of using a large amount of reference microphones. This research has important impact to test design. There is also added benefit to the accuracy of holography analysis using self-referencing instead of stationary referencing.