An Improved Temperature Index Model for Alpine Glaciers using Derived Degree-day Factors from Climatic Inputs

by

Print Friendly, PDF & Email

Durban G Keeler and Dr. Summer Rupper, Geological Sciences

Glaciers represent one of the most climatically sensitive and dynamic systems under study, and therefore have diverse implications for nations around the world. For example, Switzerland generates 56% of its power from hydroelectric facilities, many of them fed by glacial meltwater (SFOE, 2012). Many nations in the Himalayas are at risk of catastrophic flooding as glacial melt rates increase (Rupper et al., 2012). Attempts to comprehend past glacial changes can help us better understand modern changes in climate. The study of glacial melt rates over time therefore has potential regional and global significance.

One difficulty in studying and predicting glacial melt rates is the large number of variables involved, with most models necessarily including simplifying assumptions (Hock, 2003). One common method used is the positive degree-day model, or temperature index model. In this model, the total melt (M) relates to the above-freezing air temperature (T+) summed over a period of time intervals (Δt) multiplied by a proportionality factor called the degree-day factor (DDF).
1
The model is a fair approximation to actual melt records (Hock 2005) and additionally requires few onsite measurements. The degree-day factors, however, must be empirically determined for a given site (Shea, 2009). Since they can vary by nearly an order of magnitude (Hock, 2003), it is difficult to relate the results at one site to others around the world. At least one study (Braithwaite, 1995) suggests the DDFs themselves may depend on a small number of climate variables. Quantifying this dependence would allow for the determination of the degree-day factor directly from a small set of parameters in general rather than solely from empirical region-specific observations. We demonstrate a method to determine the correlation and dependence of the DDF on these different variables, and present a function to predict melt factors based on the calculated correlations. This facilitates the application of temperature index modeling to more areas with a greater level of precision and without the need for multiple in-situ measurements.

In order to obtain a sufficiently large dataset covering the full suite of glacial conditions, we used an energy balance model (EBM) to generate theoretical DDFs across a wide range of climate settings. This permitted an accurate representation of alpine glacier conditions while saving in-situ data to test the accuracy of the model. For this research, we used the MATLAB-based EBM first presented in Rupper and Roe, 2008. This model accounts for all inputs and outputs of energy into a glacial system, and calculates the total melt under those circumstances. From this calculation, we can determine the DDF over a wide range of climate settings. For our research, we assumed positive degree-days (a measure of near-surface air temperature), net incoming solar radiation (insolation), and average summertime albedo (a measure of the reflectivity of a surface) would dominate changes in DDF. All other variables were held constant at approximate global averages.

Our model generated a total of 1,602 real solutions for DDFs across all modeled climate settings. Of these, 18 were eliminated as unrealistically high (greater than 20 mm/(°C•days). Nearly all values (97.6%) fall between 0 and 5 mm/(°C•days), which is similar to values for measured melt factors in the scientific literature. Using the data from the EBM and the given ranges for positive degree-days (PDD), insolation, and albedo, we created a statistical model to predict the corresponding DDF using exploratory data analysis. We first produced an over-fitted complex linear model containing all possible combinations of our three input variables, and then reduced it to a best-fit, 10-term equation. This final function is shown in Figure 1.
2
We applied the model to randomly selected subsets of the energy balance data to determine the effectiveness and robustness of the statistical model. Such tests afford some indication of the model’s ability to predict DDFs in real data sets, and also provide a means to check for over-fitting in the model. The model performed very well in these tests, with an R2 value of over 90% at the 95% prediction interval (see Figure 2).
3
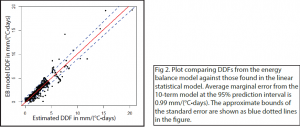
These preliminary results show promise for the use of this model in predicting degree-day factors from our chosen set of climate inputs (PDD, insolation, and albedo). One important step now is to compare the model results to melt rate data collected in the field in order to determine the models true uncertainty. Efforts to collect this data for future tests are ongoing. After these tests, our presented model could serve as an important improvement to glacier melt research, particularly when applied to areas of sparse data coverage and paleoclimate reconstructions.

Acknowledgements

Special thanks to Aaron Havens and his advisor, Dr. William F. Christensen, of the BYU Statistics Department for their assistance in building and calibrating the statistical model used in this research.

References

  • Braithwaite, R. J., 1995, Positive degree-day factors for ablation on the Greenland ice sheet studied by energy-balance modelling: Journal of Glaciology, v. 41, no. 137, p. 153-160.
  • Hock, R., 2003, Temperature index melt modelling in mountain areas: Journal of Hydrology, v. 282, p. 104-115.
  • Hock, R,. 2005, Glacier melt:a review of processes and their modelling: Progress in Physical Geography v. 29, p. 362-931
  • Rupper, S.B., and Roe, G.H., 2008, Glacier changes and regional climate – a mass and energy balance approach: Journal of Climate, v. 21, p. 5384-5401
  • Rupper, S., J. M. Schaefer, L. K. Burgener, L. S. Koenig, K. Tsering, and E. R. Cook (2012), Sensitivity and response of Bhutanese glaciers to atmospheric warming, Geophys. Res. Lett., Vol. 39, L19503
  • Shea, J. M., Moore, R. D., Stahl, K., 2009, Derivation of melt factors from glacier mass-balance records in western Canada: Journal of Glaciology, v. 55, no. 189, p. 123-130.
  • Swiss Federal Office of Energy, 2012. Hydropower: http:// www.bfe.admin.ch/themen/00490/00491/index.html?lang=en (October 2012).