Soyoung Jung and Dr. Manuel Berrondo, Department of Physics and Astronomy

Introduction

Modeling has been an important part of many fields of research. Even though it sometimes could be considered to be non-practical, it has sharpened the questions and has been a useful tool for experimental research to understand what is being observed in the laboratory. Likewise, the Heisenberg model constitutes an essential stepping stone to understand anti/ferromagnetism in magnetic materials. We have been able to develop a spin model using Landau-Lifshitz-Gilbert equation enhanced with anisotropy and long range interaction that is comparable to experimental results.

Method

The basic idea for the model is that two-spin short-range interaction of atomic magnetic dipoles can give rise to coherent long-range behavior in a lattice structure. These magnetic dipoles (spins) have fixed positions on 2D square lattice but free to rotate in any direction in 3D space. We have developed a Matlab code that evolves in time using integration methods that preserve the spin properties, mainly the length of the spin. In addition, we allow the Gilbert dissipative term considered as a driving force. Anisotropy, which means spins on the lattice have a more tendency to be affected in a certain direction is added so that we can simulate the surface of a bulk material. Anisotropy is essential in that the spin model is two dimensional but any thin magnetic material is inevitably three dimensional. Furthermore, magnetic dipole-dipole interaction was included as long-range interaction in addition to two-spin short-range interaction. This is due to the fact that all spins on the lattice essentially interact with each other even though the short-range interaction is the major interaction to govern the dynamics of the spins.

Result

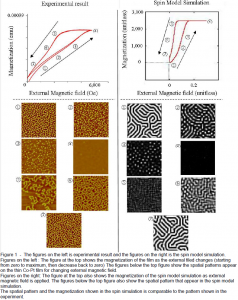
We have been able to compare the simulation using the model that we have developed with the experimental result from Chesnel’s research group at BYU. In the experiment, an external magnetic field is applied to a magnetic thin film (Co-Pt film) and the magnetic pattern on the film is observed as the strength of the external magnetic field changes. Likewise, external magnetic field is applied in the spin model that we developed. As a result, the same spatial pattern in each stage and the same pattern for magnetization was clearly observed. (See Fig.1)

Discussion and Conclusion

The spin model that we developed is a very simple model in that the method that we used in modeling only includes the vector addition and rotation operation. However, it successfully represents the real properties of magnetic dipoles (spins) on magnetic materials, which provides the possibility of using the model for research that cannot be performed experimentally.