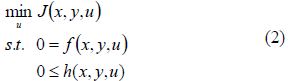Lee T. Jacobsen and Dr. John D. Hedengren
Abstract
Degradation of Solid Oxide Fuel Cells (SOFCs) can be minimized by maintaining reliability parameters during load changes. These reliability parameters are critical to maintain power generation efficiency over an extended life of the SOFC. For SOFCs to be commercially viable, the life must exceed 20,000 hours for load following applications. This is not yet achieved because transient stresses damage the fuel cell and degrade the performance over time. This study relates the development of a dynamic model for SOFC systems in order to predict optimal manipulated variable moves along a prediction horizon. The model consists of hundreds of states and parameters that permit tracking of a realistic response. Previously, this detailed model was too computationally intensive to run in parallel with the SOFC process. The contribution of this paper is an application study to enable a large-scale simulation model to be used in Model Predictive Control (MPC) without simplification. Such a technology permits real time calculation of controller moves while loads are followed during operation. The contribution demonstrates the assumptions and approach necessary to provide real-time calculations for optimal predictive control operations using a rigorous model of the SOFC process. Large-scale process models are rarely employed in real-time control because of the prohibitive computational expense necessary to complete the calculations within the specified cycle time. An efficient model based predictive controller reduces operational fluctuations related to the startup and shutdown conditions, without exceeding reliability limits in the cells.
I. INTRODUCTION
A Solid Oxide Fuel Cell (SOFC) is an electrochemical conversion device that produces electricity directly from oxidizing a fuel and uses an oxide or ceramic electrolyte material. Advantages of this class of fuel cells include high efficiency, long-term stability, fuel flexibility, low emissions, and relatively low cost. A remaining challenge is the reliability of the SOFC over a long period of time for applications that may include thermal cycling. The thermal cycling is caused by changes including start-up, shut-down, and load following. Cell damage is avoided by constraining minimum cell temperature and radial temperature gradients. The commercial requirement for reliability of stationary SOFC applications is in excess of 40,000 hours while the requirement for transient SOFC operations is in excess of 20,000 hours [1] [2]. These targets have not been achieved on a commercial scale. Several approaches are currently being researched to address the reliability limitations of SOFCs to extend the life and minimize the damage caused by load changes. One approach is to use model-based methods to better predict and identify reliability parameters that lead to degradation. If the models can be computed in parallel to the process, this gives a real-time view of the internal stresses and temperature gradients that are causing this loss of efficiency. Some of the most sophisticated and accurate models have not been applied to real-time simulation or control because of the computational burden required to complete the calculations within a specified cycle time. One method of simplification is to linearize or reduce the model complexity.
Model Predictive Control (MPC) with linear models is the most prevalent approach used for advanced multivariable control of industrial systems. In many cases, fundamental principles are not used in the development of these linear empirical models. Basic science such as material or energy balances or reaction kinetic pathways have the potential to greatly improve the performance of the controller over a wider range of operating conditions. However, relatively few of these controllers have been applied in practice because of the difficulty of constructing and solving an accurate model. The focus of this paper is on ways to apply more sophisticated and detailed models in real-time applications. In particular, this is demonstrated with an application to a well-known energy systems topic of SOFCs. Although this paper is specific to this application, the principles of obtaining and solving a rigorous model in real-time control applications are discussed for applications to other systems as well.
II. SOFC BACKGROUND AND LITERATURE REVIEW
A. SOFC Background
The cross-section of a tubular solid oxide fuel cell consists of an inner cathode layer, a middle electrolyte layer, and an outer anode layer known as the Electrode-Electrolyte Assembly (EEA). Cells are connected in series with an interconnect to build voltage in the system. This series of connected fuel cells is called a fuel cell stack. The interconnect joins the anode of one cell to the cathode of another. In the inner tube, oxygen is ionized at the cathode and oxygen ions migrate through the electrolyte where they oxidize hydrogen at the anode-electrolyte interface. This reaction releases two electrons that flow through a load back to the cathode as well as generates heat and forms water. It is necessary for SOFC’s to operate at temperatures in excess of 500⁰C in order for the cathode to be ion conductive. In addition, high temperature is required to achieve the necessary ion transport through the electrolyte for efficient SOFC operation.
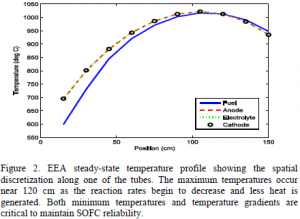
Heat is generated by the oxidation of the hydrogen reaction occurring at the anode electrolyte interface. The outer fuel side of the cell is a mixture of processed fuel and fresh fuel. Fuel sources are categorized into two types, primary and secondary fuel. The primary fuel comes from larger hydrocarbons that have been reformed by a prereformer into carbon monoxide, hydrogen, and carbon dioxide. The secondary fuel comes from fuel that has already been processed and is then recycled back to the ejector to be mixed with the primary fuel and reintroduced to the fuel cell. Further reformation reactions at the surface of the anode remove the hydrogen atoms from methane to form additional hydrogen gas. The hydrogen is then oxidized to water in the fuel cell. A ten volume discretization over 1.5 meters was used to model the tubular SOFC [3]. 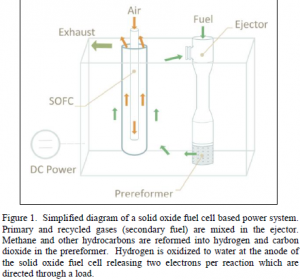 Controlling key reliability parameters is necessary for increased fuel cell lifetimes. Minimum cell temperature, maximum radial temperature gradient, steam to carbon ratio, and fuel utilization are key reliability parameters that this work seeks to constrain in a non-linear model based controller. The minimum cell temperature occurs at the fuel cell inlet. This is where primary fresh fuel first encounters the fuel cell. If frequent temperature cycling occurs below the designated minimum fuel cell temperature 1000 K, micro cracking occurs and shortens the fuel cell lifespan. Maintaining cell temperatures above the 1000 K minimum cell temperature constraint will improve fuel cell reliability.
Controlling key reliability parameters is necessary for increased fuel cell lifetimes. Minimum cell temperature, maximum radial temperature gradient, steam to carbon ratio, and fuel utilization are key reliability parameters that this work seeks to constrain in a non-linear model based controller. The minimum cell temperature occurs at the fuel cell inlet. This is where primary fresh fuel first encounters the fuel cell. If frequent temperature cycling occurs below the designated minimum fuel cell temperature 1000 K, micro cracking occurs and shortens the fuel cell lifespan. Maintaining cell temperatures above the 1000 K minimum cell temperature constraint will improve fuel cell reliability.
Another reliability parameter is the maximum radial temperature gradient. This is caused by the temperature difference between the lower temperature of the anode side gas-fuel mixture and the hotter temperature on the cathode side gases. The axial location for maximum radial temperature gradient to occur on the fuel cell is on the inlet where the lower temperature fresh fuel has been combined with recycled fuel. Spivey’s model used a nominal radial gradient of 2250 K/m [3] which is the temperature difference between the electrolyte and the anode. The highest radial gradient occurs between the electrolyte and the anode and places these two layers in tension because of expansion of the cathode. This makes the thin electrolyte layer susceptible to micro cracking and delamination inhibiting the oxygen ion transport pathway. Damaged electrolyte decreases the performance and lifespan of the fuel cell. This work seeks to constrain maximum radial gradients below 3000 K/m in SOFC control scenarios.
The ratio of steam to carbon must also be maintained to prevent carbon deposition from occurring. If enough steam is present, hydrogen production is the more favorable reforming reaction. Lack of steam can lead to coking reactions which can deposit carbon on the anode. Carbon deposition can prevent further reformation of methane into hydrogen on the anode surface. This work seeks to constrain steam to carbon ratio on a mole basis above 2:1 in control scenarios.
In addition, fuel utilization is an economic parameter but also has an indirect impact on reliability. From an economic perspective, increased fuel utilization lowers fuel pressure which leads to a lower fresh fuel requirement. This is due to the increased fuel cell temperature at the anode where further reformation reactions occur more favorably and more fuel is utilized. This also impacts reliability. If lower fuel utilization is acceptable, increased power generation can occur because increased fuel rates can be used, but the minimum cell temperature will drop due to lower fuel temperature caused by the additional fresh fuel. This decreases hydrogen production because of less reformation reactions taking place at the anode. Fuel and air utilization can indicate fuel or air starvation. If too much fuel is used and not enough oxygen ions are at the reaction site, air starvation can occur and vice versa. This can lead to oxidation occurring within the electrodes and cause cell degradation [3]. This work seeks to constrain fuel utilization above 80% in control scenarios. As indicated by the above reliability parameters, this type of control is highly non linear and interrelated. The purpose of this study is to control and optimize these non-linear relationships by solving a rigorous model in real-time fast enough to enable acceptable control for actual operation.
B. Model Predictive Control of SOFC Systems
Previous research on advanced control of SOFC systems commonly involves control of power output, voltage, temperature, steam-to-carbon ratio, or fuel/air utilization [4] [5] [6]. Often, power and temperature control are not included in the same control objective but may be in separate Single Input Single Output (SISO) loops [7] [8] [9]. Urata developed a Multiple Input Single Output (MISO) temperature controller to minimize 1D channel cell temperature variation along a planar cell; the controller adjusts fuel and air temperatures and air flow [10]. In 2009, Mueller demonstrated improved control of voltage and cell temperature variation along with faster load following using a Multiple Input Multiple Output (MIMO) Linear Quadratic Regulator (LQR) controller compared to a multi-loop SISO controller; results showed further work was needed to control mean temperature [11]. In 2011, Spivey developed a dynamic, first-principles tubular SOFC model and implemented linear MIMO Model Predictive Control (MPC) to control power output, fuel utilization, steam-to-carbon ratio, minimum cell temperature, and maximum radial thermal gradient [12]. The absolute and delta temperatures which are critical for extending SOFC lifetime along with steam to carbon ratio, fuel utilization, air utilization were held within tight constraints while power loads were met. Control objectives involved load setpoint tracking and load regulatory control subject to fuel quality disturbances.
The present work utilizes the first-principles SOFC simulator from Spivey to develop a Nonlinear Model Predictive Controller (NMPC) capable of solving in realtime. The rigorous model is composed of Partial Differential and Algebraic Equations (PDAE) that include detailed submodels of electrochemistry, heat transfer, reaction kinetics, and recycle dynamics. A general form of the model equations is shown in Equation 1 where x represents the differential model states that are discretized in time (t) and space (r and z). Additionally, y represents the algebraic model states, and u the fixed inputs or adjustable parameters. These variables are posed in open-equation format as PDAEs (f), algebraic constraints (g), or inequality constraints (h). 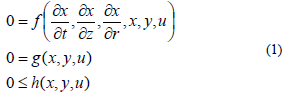 No simplification or model reduction is used in calculating the model response in the NMPC. In addition, the combination of electrochemistry, reaction kinetics, and heat transfer creates a stiff system of equations due to the separation of time-scales. While the approach of utilizing large-scale and rigorous models in real-time control is not new, the application to SOFCs is an innovation because of the nature of the stiff equations, spatial discretization in 2 dimensions, and modeling of multiple physical phenomena.
No simplification or model reduction is used in calculating the model response in the NMPC. In addition, the combination of electrochemistry, reaction kinetics, and heat transfer creates a stiff system of equations due to the separation of time-scales. While the approach of utilizing large-scale and rigorous models in real-time control is not new, the application to SOFCs is an innovation because of the nature of the stiff equations, spatial discretization in 2 dimensions, and modeling of multiple physical phenomena.
III. NOVEL APPROACH
The contribution of this paper is to apply a rigorous mathematical model of a SOFC in real-time control and optimization. This extends the former study by using the full nonlinear and dynamic model instead of the linearized dynamic version [3]. A number of challenges were addressed to make the real-time application possible including algorithmic modifications to allow the large-scale and nonlinear system to solve reliably in a deterministic timeframe. Simultaneous solution of the model equations and objective function improves the solution time over a shooting or sequential approach. The simultaneous method requires discretization in time as well as in spatial dimensions. Instead of forward time-stepping to calculate the model states, the model equations in Equation 1 are converted to a Nonlinear Programming (NLP) problem shown in Equation 2 and solved with a sparse interior point (e.g. IPOPT) or active set solver (e.g. APOPT).
The reformulation of the model equations is accomplished by posing additional equations that relate the differentials to the state variables. Orthogonal collocation on finite elements is used in this study to convert the differential system into a purely algebraic set of equations. The model at each time step has 349 variables (x, y) and 4 manipulated variables (u). When discretized over time, the number of variables is multiplied by the number of time steps projected into the future. For example, with a horizon of 100 time steps the problem has a total of 34,900 variables and 400 degrees of freedom.
IV. NON-LINEAR MODEL BASED CONTROLLER
Spivey’s modified model was solved for steady-state, dynamic, and closed loop control solutions. Dynamic and steady state solutions were validated using steady state and dynamic solutions generated by Spivey in his work. Steady state temperature profiles of the anode, cathode, electrolyte, and fuel in the axial direction of the fuel cell were evaluated. Total power response to fuel pressure moves were the basis for dynamic validation. A controller based on this model was then implemented to simulate load following scenarios. The SOFC model was then solved using the techniques mentioned in the previous section with a 10 step predictive horizon of 500 secs. A time basis of 1000 secs was used to compare responses to setpoint changes. The controller achieved power level setpoints by moving all designated manipulated variables. In addition, this model achieved desired setpoints while constraining key reliability parameters for tubular SOFCs and minimizing any deviations. These are the key reliability parameters that were identified and constrained: minimum cell temperature, maximum radial temperature gradient, steam to carbon ratio, and fuel utilization.
A. Steady State and Dynamic Model Validation
Figure 2 shows the steady state temperature profile solutions to the model. These results were obtained at simulated operating conditions of 0.63 V per cell, fuel pressure of 8.5 bar, fuel temperature of 373 K, and a system pressure of 3.5 bar. Power achieved for a single cell was 158.6 watts and a cell mass flow rate of 0.071 kg/s.
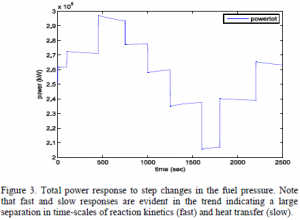
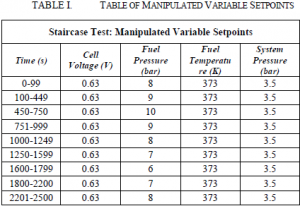
Dynamics validation was carried out by performing staircase steps with manipulated variables and observing the responses of the control variables. Figure 3 shows the total power response of the entire system to a set of staircase changes in fuel pressure. Table 1 shows the fuel pressure moves associated with the staircase test.
The simultaneous solving environment offers significant advantages in model development and testing, one of which is the speed at which solutions were obtained. Spivey’s model solved in the Simulink environment required approximately 2.5 days (3600 min) of CPU time to solve dynamic open loop solutions to manipulated variable changes whereas the results found in Figure 3 using simultaneous solution techniques required less than 2 minutes of CPU time.
B. Model Based Controller Results
Load following is a necessary attribute of a transient SOFC powered system. Practical applications of SOFC systems require the ability to change loads quickly with minimal effect on reliability. Real-time non-linear fundamental model-based control allows for larger ranges of operation within reliability parameter constraints. These model based controllers can also be tuned to minimize time to setpoint.
Figure 4 shows the total power response to a change from 260 kW high setpoint dead band to a 273 kW high setpoint dead band. The controller was able to achieve operation within the setpoint dead band in approximately four solution cycles.
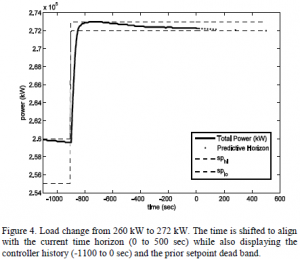 Figure 5 shows the minimum cell temperature response to the change in total power setpoint. The controller is able to constrain the minimum cell temperature as additional fresh fuel is added to achieve the new setpoint. Additional fresh fuel lowers the temperature of the fuel cell at the inlet.
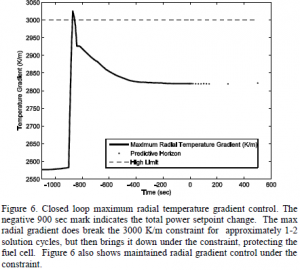
Figure 5 shows the minimum cell temperature response to the change in total power setpoint. The controller is able to constrain the minimum cell temperature as additional fresh fuel is added to achieve the new setpoint. Additional fresh fuel lowers the temperature of the fuel cell at the inlet. 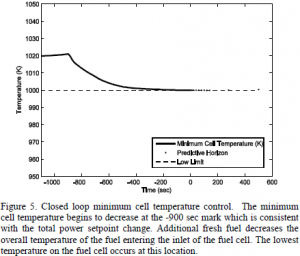 Figure 6 shows the maximum radial gradient. As indicated, the initial setpoint change increases the fuel pressure and subsequently, the amount of fresh fuel added. This causes the temperature at the anode to decrease and drives up the radial temperature gradient at the inlet. The controller recognizes this and seeks to minimize the deviation. The controller is able to bring the maximum radial gradient under the constraint in 1-2 solution cycles. Further tuning of the controller can decrease deviation time and potentially eliminate the deviation altogether. As the fuel cell increases in temperature, the gradient decreases. As more time passes, the controller is able to maintain maximum radial gradient well below the designated constraint.
Figure 6 shows the maximum radial gradient. As indicated, the initial setpoint change increases the fuel pressure and subsequently, the amount of fresh fuel added. This causes the temperature at the anode to decrease and drives up the radial temperature gradient at the inlet. The controller recognizes this and seeks to minimize the deviation. The controller is able to bring the maximum radial gradient under the constraint in 1-2 solution cycles. Further tuning of the controller can decrease deviation time and potentially eliminate the deviation altogether. As the fuel cell increases in temperature, the gradient decreases. As more time passes, the controller is able to maintain maximum radial gradient well below the designated constraint.
 The steam to carbon ratio in Figure 7 shows a large swing in response to the total power setpoint change. A deviation is shown occurring near the -900 sec mark for 3-4 solution cycles which is consistent with that change. The controller is able to recognize this deviation and bring the steam to carbon ratio back to 2:1 within 3-4 solution cycles. Further tuning would also be beneficial in reducing and eliminating deviation times.
The steam to carbon ratio in Figure 7 shows a large swing in response to the total power setpoint change. A deviation is shown occurring near the -900 sec mark for 3-4 solution cycles which is consistent with that change. The controller is able to recognize this deviation and bring the steam to carbon ratio back to 2:1 within 3-4 solution cycles. Further tuning would also be beneficial in reducing and eliminating deviation times. 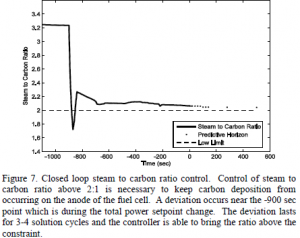 Figure 8 shows the fuel utilization response to a change in setpoint. The -1100 sec point is representative of the fuel utilization at 260 kW of power generation. Total power setpoint is increased at the -900 sec mark. As stated previously, additional fresh fuel is added and drives down the temperature of the fuel cell. The amount of reformation reactions decrease and fuel utilization decreases (see Figure 8). The controller is able to maintain fuel utilization above 80%.
Figure 8 shows the fuel utilization response to a change in setpoint. The -1100 sec point is representative of the fuel utilization at 260 kW of power generation. Total power setpoint is increased at the -900 sec mark. As stated previously, additional fresh fuel is added and drives down the temperature of the fuel cell. The amount of reformation reactions decrease and fuel utilization decreases (see Figure 8). The controller is able to maintain fuel utilization above 80%. 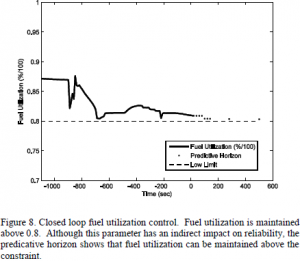 Figure 9 shows CPU calculation time for each control cycle. Each cycle calculates a 10 time step predictive horizon of 500 secs. Typical CPU calculation time varied between 15-45 secs per cycle. A real-time application would set the cycle time longer than the anticipated controller time. Setpoint changes require longer solution times as observed at cycle 30. There is an additional spike in solution time at cycle 75. The reason remains unclear and could involve fuel utilization approaching the low limit at that point.
Figure 9 shows CPU calculation time for each control cycle. Each cycle calculates a 10 time step predictive horizon of 500 secs. Typical CPU calculation time varied between 15-45 secs per cycle. A real-time application would set the cycle time longer than the anticipated controller time. Setpoint changes require longer solution times as observed at cycle 30. There is an additional spike in solution time at cycle 75. The reason remains unclear and could involve fuel utilization approaching the low limit at that point. 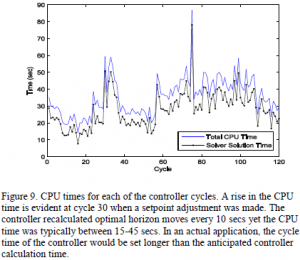
V. DISCUSSION
The plots above show the primary reliability parameters utilized in a nonlinear first principles based model controller that is solved in under one minute. Predictive horizons solved real-time in parallel with the actual system can provide insight to operators in understanding how the system will behave in response to a setpoint change long into the future. This knowledge can enable operators to take proactive action on those predictions to prevent undesirable operating conditions.
In addition, rigorous models placed in this simultaneous solving environment can be used for operator and technician training to simulate real-time scenarios. Using linear models for training scenarios such as start-up, shut-down, and unit upsets is not adequate due to the shortened range of accuracy on these types of models. Rigorous non-linear fundamental models contain much more information and can provide the dynamics necessary for a realistic simulation. In particular, the simultaneous solving techniques do not simplify and reduce the accuracy of the model in any way, but give the added advantage of significantly shortened solution times. Maintaining the known system reliability parameters within constraints would enable potential discovery of unknown contributing factors that also lead to degradation. The time required to achieve desired power levels due to load changes can now be optimized and pushed to constraint limits with reduced risk of affecting reliability i.e. minimal or no time spent in the region where SOFC degradation occurs.
The simultaneous solution generating techniques are not limited to SOFC models alone. Models from other areas can also use the same techniques to find dynamic solutions to manipulated variable changes as well as be used for model predictive control and real-time optimization. This simultaneous solution generating environment is designed to handle multiple sets of PDAEs and can generally solve systems of up to 10000 variables in one minute or less.
VI. CONCLUSION
The main contributions of this study are:
1. The demonstration of a non-linear, rigorous, fundamental principles based solid oxide fuel cell model solved in under 1 minute per cycle.
2. The demonstration of NMPC that constrains critical SOFC reliability parameters and still achieves power level setpoints.
3. The demonstration of a large-scale model containing multiple PDAE equations that can be successfully and reliably manipulated and solved with a simultaneous approach. Real-time non-linear model predictive control can significantly improve the reliability of current SOFCs by effectively constraining key reliability parameters while optimizing an SOFC process to produce the desired power level output. A wider range of control can be utilized to extend the safe operating limits of an SOFC system and enable additional optimization by using simultaneous solving techniques on a rigorous non-linear fundamental principles based model.
ACKNOWLEDGMENT
We would like to acknowledge the contributions and helpful feedback of Ben Spivey, Aswin Venkat of Bloom Energy, and Larry Chick of Pacific Northwest National Labs.
REFERENCES
- H. Yokokawa and H. I. B. M. A. Tu, “Fundamental mechanisms limiting solid oxide fuel cell durability,” Journal of Power Sources, vol. 182, no. 2, p. 400–412, 2008.
- H.-T. Lima, S. C. Hwang, Y. M. Park and I. S. Lee, “Performance and long term stability of large area anode supported solid oxide fuel cells (SOFCs),” Solid State Ionics, p. Online, 2012.
- B. J. Spivey, Dynamic Modeling, Model-Based Control, and Optimization of Solid Oxide Fuel Cells, Austin, Texas: The University of Texas at Austin, 2011.
- M. Fardadi, F. Mueller and F. Jabbari, “Feedback control of solid oxide,” Journal of Power Sources, pp. 4222-4233, 2010.
- H. Huo, X. Zhu, W. Hu, H. Tu., J. Li and J. Yang, “Nonlinear model predictive control of sofc based on a hammerstein model,” Journal of Power Sources, vol. 185, pp. 338-344, 2008.
- F. Jurado, “Predictive control of solid oxide fuel cells using fuzzy hammerstein,” Journal of Power Sources, vol. 158, pp. 245-253, 2006.
- P. Aguiar, C. Adjiman and N. Brandon, “Anode-supported intermediate-temperature direct internal reforming solid oxide fuel cell ii. model-based dynamic performance and control,” Journal of Power Sources, vol. 147, pp. 136-147, 2005.
- R. Kandepu, L. Imsland, B. Foss, C. Stiller, B. Thorud and O. Bolland, “Modeling and control of a sofc-gt-based autonomous power system,” Energy, vol. 32(4), pp. 406-417, 2007.
- C. Stiller, B. Thorud, O. Bolland, R. Kandepu and L. Imsland, “Control strategy for a solid oxide fuel cell and gas turbine hybrid system,” Journal of Power Sources, vol. 158, pp. 303-315, 2006.
- Y. Inui, N. Ito, T. Nakajima and A. Urata, “Analytical investigation on cell temperature control method of planar solid oxide fuel cell,” Energy Conversion & Management, vol. 47, pp. 2319-2328, 2006.
- F. Mueller, F. Jabbari, S. J. Brouwer and H. Ghezel-Ayagh, “Linear quadratic regulator for a bottoming solid oxide fuel cell gas turbine hybrid system,” Journal of Dynamic Systems, Measurement, and Control, vol. 131, pp. 1-9, 2009.
- B. Spivey and T. F. Edgar, “Dynamic modeling, simulation, and MIMO predictive control of a tubular solid oxide fuel cell,” Journal of Process Control, vol. 22, no. 8, pp. 1502-1520, 2012.