Blaine Harker and Drs. Kent Gee and Brian Anderson, Dept. of Physics and Astronomy
Time reversal is a relatively new type of acoustic localization with many applications, such as lithotripsy to destroy kidney stones, and secure underwater sound communication, though in some ways time reversal is still in the development stage. To this end, we explore the efficiency and limitations of this technique due to the number of sensors used and the directivity pattern of the source to be reconstructed in the experiment.
Imagine a pebble dropped into a pond. Circular ripples spread out away from the drop location. If one were to play the movie backwards in Time, the ripples would converge at the drop location, recreating the initial disturbance caused by the pebble. This is the essence of the TR technique. Extending this to acoustics, transducers (i.e. microphones and speakers) act to receive, reverse and retransmit the waveform so that it is re-collected at the original source location. According to M. Fink, spatial sampling at λ/2 transducer spacing is necessary to avoid grating lobes, however less so if the mirror is pre-focused on the sourcei. Often the source location is known to within a certain extent. In order to develop better criterion for a time reversal experiment, we optimize the number of transducers needed given a relative knowledge of the source location. In optimizing the experiment we find that time reversal can effectively localize a simple source broadcasting a continuous wave dependent on angular spacing. Furthermore, the aperture of the time reversal mirror (TRM) is the most important parameter when creating a time reversal setup for imaging a source.
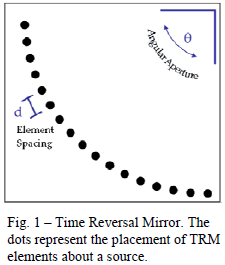
In order to optimize our tests, the experiments were carried out computationally to allow for rapid parameter changes. A simple source is placed in a half-space environment and spherically propagates a continuous sine wave. Next, microphones are placed around the experiment in multiple fashions to test how well the time reversal process could locate the original source. In order to better understand how microphone placement affects time reversal, we experimented upon six different parameters: angular aperture, TRM element spacing, relative knowledge of the source location, frequency, TRM shape, and TRM radius. As shown in Figure 1, the aperture is the angle that the TRM sweeps around the source. The TRM element spacing is the number of microphones within a given angular aperture. A relative knowledge of the source location is categorized by a certain area within which the source is known to be positioned (e.g. 5λ by 5λ square region). The frequency parameter simply alters the point source sine-wave. The TRM shape experiments with different shapes. Finally, the TRM radius is the manipulation of the radius of the elements from the source location. In this final parameter, the source was also moved off-axis so as not to always be centered geometrically in the TRM. In order to quantify the effect that varying any one of these parameters had on the experiment, two quality metrics were developed. During the backward propagation, the pressure at the original source location is measured and compared to the field average to give a source to field ratio. Also, the pressure at the source location is compared to the next highest amplitude in the field. This was referred to as the source to next peak ratio. These two metrics quantified the results in an easy to analyze way in order to compare hundreds of different scenarios.
After analyzing we found that the parameters which affected our results the most were the angular aperture and the angular TRM element spacing. The latter showed that there was a limit to the quality of localization that could be achieved (see Figure 2(a)). Adding more microphones to the experiment beyond this limit did not increase the quality factor. Another interesting feature was that the element spacing, or rather this density of elements per unit angle, had an upper limit regardless of the angular aperture size. Although the overall quality was improved by increasing the angular aperture as shown in Figure 2(b), the trend was similar across each trial. In Figure 2(c) these different angular coverage are shown normalized to show the similarity among each angular coverage trial. This provided evidence that overall quality increased proportional to the angular coverage, and that the angular density of TRM elements was the most important parameter to consider when optimizing a Time Reversal experiment. By adding more transducers given a certain angular aperture, an upper limit can be calculated, thus allowing for the most efficient use of resources in the experimental setup. In many cases the necessary number of transducers is well below the number used in a λ/2 spacing setup.
This research has been presented for multiple events. In May 2011, the author gave an invited presentation at the Acoustical Society of America (ASA) research conference in Seattleii. In November of the same year he gave a follow-up poster presentation at the ASA San Diego meetingiii. The research was presented on BYU’s campus during the 2011 Spring Research Meeting and the Royster Poster Competition the December of that year. The author is preparing an honor’s thesis on time reversal which will also be the manuscript for a journal article to be submitted in summer 2012 for review. The new questions raised and research opportunities from this study have opened new opportunities to gain insight and knowledge.

References
- M. Fink, “Time reversed acoustics,” Phys. Today 50, 34-40 (1997).
- Harker, B. M. and B. E. Anderson (2011). “Optimizing time reversal mirrors in a half-space environment with application to localization of jet noise.” The Journal of the Acoustical Society of America 129(4): 2532-2532.
- Harker, B. and B. Anderson (2011). “Application of time reversal to sources in non-ideal environments.” The Journal of the Acoustical Society of America 130(4): 2430-2430.