Julius Adebayo and Dr. Sean Warnick, Computer Science
A system-level understanding of the functioning behavior of a cell requires an accurate representation of the underlying networks of gene and protein interactions. Network reconstruction is an area of systems biology that attempts to reconstruct the network of regulatory interactions from available measurements using a mathematical framework. Developing a theoretical relationship between Bayesian inference methods and dynamical structure functions is an important first step in developing unique qualitative processes that correctly infer network structures [1], [3].
Bayesian networks (BN) are interpretable and flexible models for representing probabilistic relationships between multiple interacting entities. In this case, reconstruction is done through analysis of linear state space models (VBSSM). Another reconstruction method is through the use of dynamical structure functions (DSF). In conducting this research, I sought to compare the performance and verification analysis of the fundamental assumption in the VBSSM inference method with pre stated conditions from the DSF method. This is because in previous work done on DSF [1], it was established that certain assumptions, that is, independent perturbations of individual species involved in a given reconstruction experiment had to be performed in order to reconstruct. This analysis was to figure out how Bayesian inference methods, especially the VBSSM inference methods were meeting these different conditions in order to reconstruct the different networks that are obtained.
This analysis is essential because there are different network reconstruction algorithms available to biologists intending to design efficient drug targets and perform analysis of systems. In order to develop adequate algorithms that efficiently answer and provide robust solutions to these questions, a comparison of algorithms has to be performed. In conducting this research, I developed a modified toolbox for the VBSSM method in order to adequately simulate its conditions and reconstruction of networks. In doing this, I got a fundamental understanding of the mathematical theory behind the reconstruction method. Having studied DSF for a while, an implementation of the DSF method was already available. An in silico model of a network allows for a comparison to be made under controlled conditions.
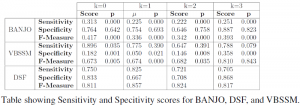
By performing mathematical analyses and simulations, it was discovered that the stated assumption by DSF was being met by the Bayesian systems studied. In the particular case of VBSSM, the overall definition of the algorithm involved in silicon perturbation with white noise vectors in order to differentiate different state measurements. Initially, this was not obvious because such assumption, especially when the magnitude of the individually orthogonal noise vectors is small, does not significantly change the value of the measurements and the transfer functions obtained. However, in simulation and results obtained, it was noted that the orthogonality of the noise vectors perturbing different states as well as their relatively high magnitude essentially met the reconstruction condition indicated by DSF [1], [2] and [3]. These analyses essentially solved the main question of the proposal. However, in order to go ahead, I went on to analyze the performance of the VBSSM method in order to fully understand and get a sense for how powerful the VBSSM method is. Results from this comparison are shown in table below.
Indicated in the above table are scores showing the sensitivity, specitivity as well as the FMeasure which indicates how precise the network obtained was for any given analysis [3]. The results above compare the networks obtained from reconstruction in the case of VBSSM, BANJO and DSF under different hidden state conditions. This test served to show how robust each of these different methods are.
This research experience helped me to understand the essence of the scientific inquiry, and to know how difficult it can sometimes be to analyze and synthesize other people’s scientific discoveries. This experience also enriched me by giving me the opportunity to study concepts and ideas that are very exciting in the field of computational biology. In studying these things, I have developed a firm sense of understanding and appreciation for the study of biochemical systems using computational tools. Finally, the results from this research have led to a paper being published in an IEEE Journal and would serve as a portion of my honors thesis.
Sources
- E. Yeung, B. Durtschi, and S. Warnick “A comparison of network reconstruction methods for chemical reaction networks.” Foundations of Systems Biology and Engineering, 2009.
- D. Husmeier, “Probabilistic Modeling in Bioinformatics and Medical Informatics.” Springer, 2005.
- Jing Yu, V. Anne Smith, and Erich D. Jarvis, “Advances to Bayesian Network inference for generating causal networks”, Duke University Medical center.