Jeffrey Hendricks and Dr. Tadd Truscott, Department of Mechanical Engineering

The study of fluid flow on a microscale has become of increasing interest in recent years. We have studied the effects of capillary action in a micro-channel with a rectangular cross-section having a large width to height ratio. In general, capillary action allows fluid to fill a horizontally oriented tube smaller than the capillary length (on the order of 2 mm in water). When the far end of such a tube is capped, typically the fluid is drawn through the tube until it meets a pressure field that is equal but opposite of the surface tension force. We have found that when the capillary cross-section is rectangular with a large width to height ratio, the fluid can pass by the pressure field on the narrower sides of the capillary allowing fluid to move into the narrow gap while leaving pockets of air in the wake (figure 1).

Achieving a better understanding of this phenomenon would have important applications. In particular, understanding this occurrence could enhance our ability to apply antibiotics after the shaping of a root canal, draw fluid into small mechanisms for lubrication and non-corrosive coatings, and enhance fluid transport in man-made porous materials.

Our initial approach was to modify existing theory on capillarity. In particular we sought to generalize the theory of Washburn who, in 1921, derived an analytical expression for the rate of penetration into a small, horizontally oriented capillary tube. We found that we first needed a better understanding of the relationship between pressure and the geometry of the fluid.

While capillary action is well explained for circular cross-sectional capillaries, it is not as well understood for non-axisymmetric capillaries. Phan et al. (2010) explored capillary filling for rectangular, closed-ended nano-channels and focused largely on effects of gas absorption. More recently, Hilpert (2009) generalized Washburn’s results by accounting for a dynamic contact angle. We have focused on the relationship between the pressure and the fluid meniscus.

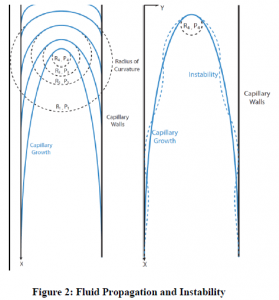
Due to the surface tension of the fluid, it will tend to minimize the surface area of the meniscus. For the fluid imbibing along the corner of the channel, the minimal surface for a particular cross-section is a catenary. The catenary will be uniquely defined by the contact angle of the fluid with the channel surface and the amount of fluid imbibed at that cross-section. We see that, along the side of the channel, the catenaries in each corner must at some point meet. It is at this point that we believe an important instability occurs. When the two catenaries meet, the fluid meniscus must change shape and allow for a sudden increase of flow along the channel side. This instability will propagate as a wave down the length of the channel.

Next we consider the meniscus and pressure relationship at the center of the channel. This relationship will be governed by the Young-Laplace equation which states that the change in pressure is inversely related to the radii of curvature of the meniscus. Thus, as the fluid moves down the channel, the pressure increases and the radius of curvature decreases. In the corners, however, the fluid front remains relatively flat and is thus able to continue to flow. As a result we end up with geometry as in Figure 2 which contributes to the eventual pinch-off.

In particular, this decreasing central radius, along with the continued flow in the corners and propagating instability along the sides, can explain pinch-off. We can view it as a mechanism very similar to the Rayleigh-Plateau instability. In the case of Rayleigh-Plateau, small perturbations on the surface of a liquid jet result in a wave instability causing the jet to pinch off into drops. The situation we have developed is similar. Like Rayleigh-Plateau, there is a liquid-air interface with a wave disturbance at the meniscus.

Just as with the Rayleigh-Plateau instability, the disturbance will grow. As these waves increase in amplitude, the radius of the
central meniscus also decreases. Together, these will lead to pinch-off. Pinch-off will decrease the pressure on the fluid front
allowing it to continue to move down the channel. This process repeats until the fluid has entirely coated the inside of the channel.

While there is much more research that can be done in this area, the work we have done to this point should add significant understanding to the study of this complex physical phenomenon. We gave an oral presentation of the results of our research at the 2011 Utah Conference of Undergraduate Research held at Weber State University. We are hopeful that the progress we have made will eventually contribute to a publication.

References

• M. Hilpert, “Effects of dynamic contact angle on liquid infiltration into horizontal capillary tubes: (Semi)-analytical solutions”, Journal of Colloid and Interface Science, vol. 337, pp. 131, 2009.
• Phan, V.; Nguyen N.; Yang C.; Joseph, P.; Djeghlaf L.; Bourrier D.; Gue A.; “Capillary Filling in Closed End Nanochannels”, Langmuir, vol. 26 (16), pp. 13251.
• E. Washburn, “The Dynamics of Capillary Flow”, The Physical Review, vol. 17, pp. 273, 1921.