Rachel Suggs and Dr. Tyler Jarvis, Department of Mathematics

Suppose you have a physical system that can jump suddenly between two stable states. Then a function modeling the system will have a singularity at the jump. Our singularities will all be dened by polynomials, such as x3y + y5 + z2. Mathematician V.I. Arnol’d studied such singularities in an abstract setting, and he noticed that a certain 14 singularities came in pairs: numbers describing two dierent aspects of these singularities matched each singularity with its \dual” partner, which had the same numbers but with reversed roles (see Table 1). Arnol’d found no mathematical or physical reason why these singularities should be partnered in this way; hence, he dubbed the phenomenon a strange duality. This duality has fascinated mathematicians ever since, prompting explanations from multiple branches of mathematics.

Several years later, a second type of duality arose in a completely dierent way. This duality was rst proposed by string theorists searching for the fundamental nature of the universe. String theory calls for six extra spatial dimensions which are \curled up” in the form of Calabi-Yau manifolds, which, like singularities, are dened by polynomials. No one knows what the exact form of the extra dimensions should be. However, string theorists have conjectured that certain \dual” pairs of Calabi-Yau manifolds should yield identical physical, and hence mathematical models. These dual pairs are then said to exhibit mirror symmetry.

Mirror symmetry intrigues mathematicians, who have been working on a formal proof of its existence ever since its discovery. Unfortunately, Calabi-Yau manifolds are extremely difficult to work with. Recently interest has developed in Landau-Ginzburg constructions, which promise to exhibit the same mirror symmetry as Calabi-Yau manifolds. Current research in Landau-Ginzburg mirror symmetry focuses on showing that duality holds here, and that it is mathematically equivalent to the duality of Calabi-Yau manifolds. Researchers have already proved several aspects of both problems. Once such connections are established, results in Landau-Ginzburg mirror symmetry can be used to solve problems in Calabi-Yau geometry, a much harder area of mathematics.

A few years ago, while working on his dissertation in Landau-Ginzburg mirror symmetry, Marc Krawitz noticed that the dual pairs of strange duality and Landau-Ginzburg mirror symmetry coincide; that is, a singularity’s strange dual is also its mirror symmetry partner [1]. This is a totally unexpected connection. Though singularities have physical interpretations, strange duality is a purely mathematical phenomenon; on the other hand, mirror symmetry arises from a physical situation and has only been partially validated mathematically. In some sense, strange duality is a proof without a picture, and mirror symmetry is a picture without a proof. Understanding the relationship between these two dualities will provide insight into both singularity theory and Landau-Ginzburg mirror symmetry.

The goal of this project was to nd results that will contribute to our understanding of that relationship. Specically, my goal was to unravel a technicality concerning the denitions of strange duality and mirror symmetry. The technicality is that both strange duality and mirror symmetry actually deal with classes of polynomials, not individual polynomials. Moreover, the classes of polynomials involved in each duality are not exactly the same (and Krawitz’s result is not really as clean as I stated it above). The rst task, then, is to understand the relationship between the strange duality classes and the mirror symmetry classes. The second task is to see whether this information adds any insight to Krawitz’s argument. As outlined in my proposal, I successfully completed both these tasks. The results are presented in my honors thesis [2].

Strange duality classes of polynomials are determined by what is called analytic equivalence; mirror symmetry classes, on the other hand, are determined by the weights of the polynomial. Our rst task, then, is to understand the relationship between the analytic equivalence class and the weights of a polynomial. I discovered this relationship using published results from multiple journals. From [3], I learned that if two polynomials are analytically equivalent, they will always have the same weights. In other words, if two polynomials are in the same strange duality class, then they are also in the same mirror symmetry class. From [4], I found a lemma enabling me to prove that for all polynomials involved in strange duality, the converse is also true: polynomials with the same weights are analytically equivalent. In general this is not true; I found an example of two polynomials (not used in strange duality) with the same weights that are not analytically equivalent.

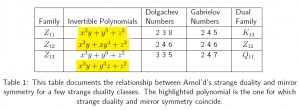
Because it is much easier to nd all polynomials with a given set of weights than it is to nd all polynomials in an analytic equivalence class, these results are very helpful. Using these results and some Sage computer code, I was able to nd exactly what all the polynomials in the strange duality classes are. In Table 1, I have listed a few strange duality classes and then all of the polynomials in that pile (which satisfy certain properties we care about).

Using this list, I was able to explore Krawitz’s proof of a connection between strange duality and mirror symmetry. His proof was to nd exactly one polynomial for which the two dualities coincided; however, he did not answer the question as to whether there are other possibilities. As demonstrated in Table 1, I found that Krawitz in fact found all such polynomials.

The natural next step to this project is to nd a more conceptual explanation of the relationship between strange duality and mirror symmetry. Strange duality is actually dened in terms of numbers called the Dolgachev and Gabrielov numbers of the polynomial. Hence, this step would likely involve an explanation of the Dolgachev and Gabrielov numbers in terms of mirror symmetry.

References

1. Marc Krawitz. FJRW rings and Landau-Ginzburg Mirror Symmetry. PhD thesis, University of Michigan,
   2010.
2. Rachel Suggs. An explanation of strange duality in terms of Landau-Ginzburg mirror symmetry. Brigham
   Young University Honors thesis, Aug. 2012.
3. Kyoji Saito. Quasihomogene isolierte Singularitaten von Hyper achen. Invent. Math., 14:123{142, 1971.
4. V. I. Arnol0d. Normal forms of functions in the neighborhood of degenerate critical points. Uspehi Mat.
   Nauk, 29(2(176)):11{49, 1974.