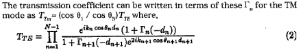Travis Elgin Oliphant, Department of Electrical and Computer Engineering

Introduction

The Interaction of Gaussian beams with multi-layer dielectric structures has been the subject of numerous studies since Goos and Hiinchen first reported their findings [1]. In addition, resonant tunneling has been a source of considerable investigation both as It applies to quantum electronics and with regard to electromagnetic phenomena. Transistor [2] and a waveguide polarizer [3] have been suggested to take advantage of the resonant tunneling effects of a plane-wave impinging on a multilayer dielectric. The purpose of this study is to further examine the possibility of such applications of resonant tunneling phenomena by extending the analysis to finite width beams. Specifically, this research focuses on the behavior of two-dimensional Gaussian beams at five-layer dielectric structures used in resonant-tunneling applications. This report provides a brief synopsis of some of the results contained in an Honors thesis submitted to Brigham Young University in July, 1995[4].

A two-dimensional monochromatic Gaussian beam is Incident on a five-layer dielectric str!-Icture, infinite in x with the first and last layers semi-Infinite in z. Figure 1 shows the geometry of the problem. Spatial Fourier analysis and the property of superposition are used to decompose the Gaussian beam into component plane-waves whose reflection and transmission coefficients can be independently calculated. The resulting reflected and transmitted beams are thus computed as a superposition of plane-waves weighted by these coefficients. The approach taken is similar to the investigations of past researchers, and a detailed discussion can be found in [5].

In order to perform the calculations, however, we used the fast Fourier transform instead of numerical integration to calculate the profiles of the reflected and transmitted beams. In other words, samples of the spatial (angle) spectrum of the incident Gaussian beam are estimated using the FFT. These are scaled by the plane-wave reflection and transmission coefficients for the five-layer structure. These samples are then used to estimate samples of the transmitted and reflected beams through the inverse fast Fourier transform.

Evaluating the plane-wave transmission and reflection coefficients for a five-layer structure is straight-forward. Our derivation used the transmission- line analogy wherein boundary conditions are enforced at the interfaces through the use of wave-impedances in each medium. These impedances are then forced to be continuous at the boundaries as required by Maxwell’s Laws. Specifically, the reflection coefficient, 11, is computed recursively using

where rn.J,n is the Fresnel Reflection coefficient corresponding to a TE or TM mode, d., is the thickness of the n'” layer, and I’5(-d5) = 0.

Results and Discussion

The Honors thesis on which this report is based actually investigates both the waveguide polarizer and the optical transistors. Since the results are similar for both devices, this synopsis only describes results obtained for the optical transistor. The optical transistor was suggested by Vigoureaux and Raba and has the following specifications: n1 = n5 = 2.4, n, = n4 = 1.6, and region 3 is a nonlinear CdS layer whose index of refraction can vary from 2.64 to 2.66 depending on the power density of light in region 3 [2]. In addition, the thicknesses of the three intermediate layers are d2 = d4 = 100nm and d3 = 490.1nm. The incident light is at an angle of 70′, has a free-space wavelength of 530nm, and has a beam width of 0.2mm. Figure 2a shows the incident TE beam magnitude profile (in a cross section perpendicular to the direction of travel) together with the profile (along the last boundary) of the transmitted beam for four values of the index of refraction of region 3. This figure indicates that by modulating the index of refraction of the middle region by 0.76%, transmissivity of the device can be altered from 100% to 16%, thus demonstrating the feasibility of the design for finite-width incident beams.

One Important fact must not be overlooked: the Gaussian beam will only be transmitted as a Gaussian beam if it is wide enough so that each component in the angular spectrum sees a similar transmission coefficient. If the angular (spatial) variation of the beam is of the same order as or less than that of the transmission coefficient, then beam-deformation occurs. The bottom figure in figure 2a shows one possible deformation due to thick evanescent regions. Although beam deformation may be undesirable in an optical transistor, its possibility does indicate that resonant-tunneling effects could be used in beam-shaping devices.

To further examine the issue of beam-deformation it must be understood how the plane-wave transmission coefficient varies with incidence angle so that an understanding of how each spatial frequency composing the Gaussian beam is transmitted. Figure 2b shows how the transmission coefficient varies with incidence angle for several values of d2 = d4.

Notice that peak transmission occurs at higher incidence angles for smaller thicknesses of the evanescent regions. More importantly, however, this figure reveals that thicker evanescent regions produce narrower angular transmission bands. Thus, since the width of the beam is inversely related to its angular spectral width, thicker evanescent regions mean that wider beams must be used to take advantage of the angular effects and avoid beam deformation.

Conclusion

In conclusion, we have presented a method for determining the transmitted beam through a resonant-tunneling structure for an incident beam with Gaussian profile. In addition, we have demonstrated the feasibility of an optical transistor using finite width laser-beams and have discussed implications of the finite width of the beam on choosing the thickness of the evanescent regions to avoid beam deformation. The results presented here also suggest that beam-shaping can be performed using resonant-tunneling effects.

References

1. A. Purl and J, L. Birman, “Goos-Hanchen beam shift at total internal reflection with application to spatially dispersive media,” Journal of the Optical Society of America A, val. 3, pp. 542-543, 1986.
2. J. M. Vigoureaux and F. Raba, “A model for the optical transistor and optical switching,” Journal of Modern Optics, val. 38, no. 12, pp. 2521- 2530, 1991.
3. K. Thyagarajan, S. D. Seshadri, and A. K. Ghatak, “Waveguide polarizer based on resonant tunneling,” Journal of Lightwave Technology, val. 9, pp. 315-317, March 1991.
4. T. E. Oliphant, “Resonant tunneling of gaussian beams,” Honors thesis, Brigham Young University, July 1995.
5. C. W. Hsue and T. Tamir, “Lateral displacement and distortion of beams incident upon a transmitting-layer configuration,” Journal of the Optical Society of America A, vol. 2, pp. 978-987, June 1985 .