Jared Fisher and Dr. Gilbert Fellingham, Department of Statistics

Most measurements follow trends over time, and those trends can be modeled. While there are many techniques for doing this, this project’s model brings a unique angle. This method can model trends with multiple peaks, from different subjects, and group them in clusters of similar curves. This permits inference on behalf of the scientist as to what is similar between subjects within a group. We have applied this algorithm to data from Major League Baseball, due to its rich nature. We hope to draw a conclusion as to who the greatest batter of all-time is, discover which players might be undiscovered steroid users, and see what events in baseball history had lasting effects on the game.

We have found that in the realm of Major League Baseball, the majority of players follow one of a set of synonymous hitting patterns over the course of their career. The aforementioned grouping piece of this algorithm is called a Dirichlet process, and with it we hope to find the trend groups that the players fall into. However, because changes in batting performance could be due to a number of factors, we also take into account other measurable parameters. Certain years in baseball history are marked by rule changes, which could help or hurt all batters in general. Also, a player may switch teams and play that season’s home games on a field with different back wall heights or distances. This, of course, changes the height and/or distance needed for a homerun. Moreover, players from different eras tend to play under different strategies. Lastly, and most basically, the player’s personal batting ability may simply improve or even falter throughout their career. Yet, as it could be a combination of these, all of the above mentioned variables are taken into account, similar to the work of Berry, et al (1999).

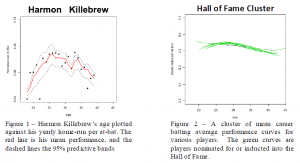
It is common to see a rise and fall of both hits per-at-bat (batting average) and home runs per-at-bat; as one might guess, a player tends to peak in the middle of his career. However, some players seem to have two peaks in their batting performances. This means a single player’s career hitting performance can be modeled by a quartic (4th degree) polynomial, as it allows for two peaks. We model this using every player’s batting average and home runs per-at-bat for every year of his career, represented below by p_ij, where p is the probability of getting a hit when at bat, for player i in year j (let all i’s and j’s thus denote). Because probabilities are restricted between, we take the logit function, or log odds, of , to allow the model to use the full real number line. Age is designated as x_ij for player i in year j. Each B’ is a polynomial coefficients. Era effect, the added value from player i being born in a given decade, is represented by d_i. The effect of any given year is y_ij and b_ij is the ballpark effect.

Using a Bayesian non-parametric technique, the Dirichlet process, we estimate the five B coefficients. Over an iterated computer algorithm, known as Markov chain Monte Carlo, this process allows the coefficients of players to mimic others’, forming groups among the players. These groups are unbiased by any effects presented by era, year or ballpark as those are also measured. A Bayesian parametric approach called Metropolis-Hastings, allows us to estimate all of the effects.

This algorithm is programmed in a lengthy, compiled FORTRAN script, and takes nearly a week to compute over 19,000 parameters for the almost 4,000 players. Due to this complexity, various tweaks must still be made to ensure proper and correct convergence of the parameters, thus our final conclusions are yet to be made. However, the parametric and non-parametric pieces do work smoothly when separated. While parametric methods are well documented, nearly a year was spent configuring the Dirichlet process and analyzing the output to correctly estimate and cluster the coefficients. This phase of the project culminated in a visit to the 2011 New England Symposium on Statistics in Sports (NESSIS) in September of 2011.

This non-parametric algorithm creates some groups of players that are largely Hall of Fame candidates or that have several known steroid-users, suggesting that others in the group might have similar traits. See figure 2 below for an example of such a group. Another strength afforded by this methodology is its ability to provide significant inference to the scientist as to the possible future performance of young players. These traits and many others can and will be forwarded on to other important fields such as economics and medicine, promising significant results to all. This is precisely why, upon completion, this project will not only be published in a prestigious, peer-reviewed, statistical journal, but applied to various other data sets as well.

Special thanks to the National Science Foundation and IMPACT (Grant #0639328), Dr. C. Shane Reese and Kristopher R. Young.

References

• Berry, S. M., C. S. Reese, and P. D. Larkey. “Bridging Different Eras in Sports”, JASA, 94(447):661-686, 1999.